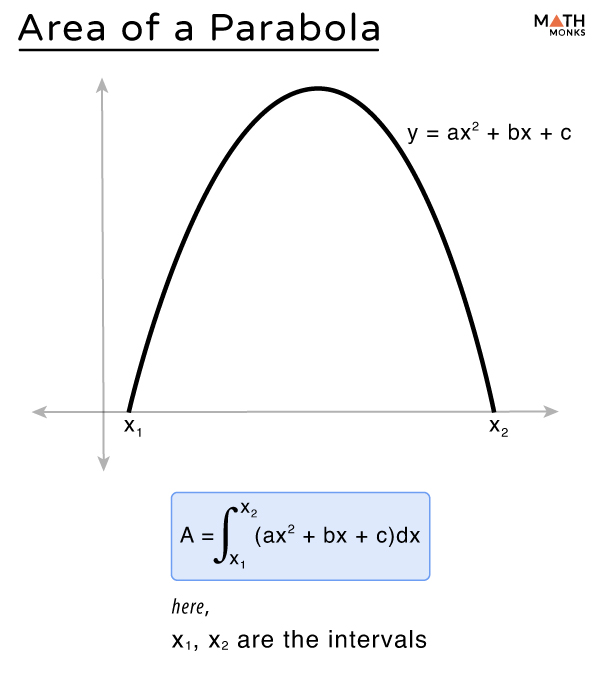
The area under a parabola refers to the space enclosed between a parabola and the x-axis, typically over a given interval.
Formulas
Since a parabola extends indefinitely, it can be obtained by integrating the general quadratic function y = ax2 + bx + c (which represents a parabola).
On integrating the function y = ax2 + bx + c within the limit x = x1 to x = x2 (definite integral), we get
${A=\int ^{x_{2}}_{x_{1}}\left( ax^{2}+bx+c\right) dx}$
⇒ ${A=\left[ \dfrac{a}{3}x^{3}+\dfrac{b}{2}x^{2}+cx\right] _{x_{1}}^{x_{2}}}$
Solved Examples
![]()
Calculate the area under the parabola y = 2x2 + 3x + 1 between x = 0 and x = 2.
Solution:
![]()
Given, y = 2x2 + 3x + 1
As we know, the area of the parabola is ${A=\int ^{x_{2}}_{x_{1}}\left( ax^{2}+bx+c\right) dx}$
Here, x1 = 0 and x2 = 2
Now, ${A=\int ^{2}_{0}\left( 2x^{2}+3x+1\right) dx}$
= ${\left[ \dfrac{2x^{3}}{3}+\dfrac{3}{2}x^{2}+x\right] _{0}^{2}}$
= ${\left( \dfrac{2\left( 2\right) ^{3}}{3}+\dfrac{3}{2}\left( 2\right) ^{2}+2-\dfrac{2\left( 0\right) ^{3}}{3}-\dfrac{3\left( 0\right) ^{2}}{2}-0\right)}$
= ${\left( \dfrac{16}{3}+6+2\right)}$
= ${\dfrac{40}{3}}$
Thus, the area of the parabola is ${\dfrac{40}{3}}$ square units.
![]()
Find the area under the parabola described by the function y = 3x2 + 2x + 1 between x = 1 and x = 4 using the integration method.
Solution:
![]()
Given, y = 3x2 + 2x + 1
As we know, the area of the parabola is ${A=\int ^{x_{2}}_{x_{1}}\left( ax^{2}+bx+c\right) dx}$
Here, x1 = 1 and x2 = 4
Now, ${A=\int ^{4}_{1}\left( 3x^{2}+2x+1\right) dx}$
= ${\left[ \dfrac{3x^{3}}{3}+\dfrac{2}{2}x^{2}+x\right] _{1}^{4}}$
= ${\left[ x^{3}+x^{2}+x\right] _{1}^{4}}$
= (4)3 + (4)2 + 4 – (1)3 – (1)2 – 1
= 81
Thus, the area of the parabola is 81 square units.
Problem – Finding the area of a parabola when the CHORD LENGTH and the LENGTH OF AXIS OF SYMMETRY are given.
The formula for the area of a parabola is:
${A=\dfrac{2}{3}bh}$
Here,
b = length of chord,
h = length along the axis of symmetry
It is applied in specific parabolas, which are symmetric about the x-axis or the y-axis.
![]()
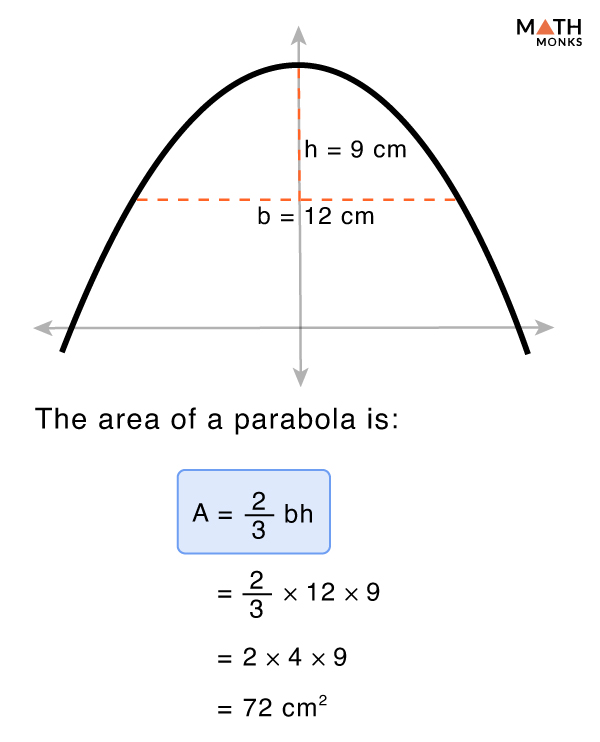
A parabola has a chord with a length of 12 cm, and the height from the chord to the vertex along the axis of symmetry is 9 cm. Calculate the area of the region enclosed by the parabola and the chord.
Solution:
![]()
A parabolic arch has a chord that is 15 meters long, with a height of 10 meters from the midpoint of the chord to the vertex along the axis of symmetry. Calculate the area enclosed by the parabola.
Solution:
![]()
As we know, the area of a parabola is ${A=\dfrac{2}{3}bh}$
Here,
b = 15 meters
h = 10 meters
Thus, the area enclosed by the parabola is
${A=\dfrac{2}{3}\times 15\times 10}$
= ${2\times 5\times 10}$
= ${100}$ square meters
Thus, the area enclosed by the parabola is 100 square meters.
![]()
If the area of a parabola is 72 square units, and the height along the axis of symmetry is 6 units, find the length of the chord.
Solution:
![]()
As we know, the area of a parabola is ${A=\dfrac{2}{3}bh}$
Here,
A = 72 square units
h = 6 units
Thus, the length of the chord is
${72=\dfrac{2}{3}\times b\times 6}$
⇒ 72 = 4b
⇒ b = 18
Thus, the length of the chord is 18 units.
