Last modified on November 19th, 2024

chapter outline

 

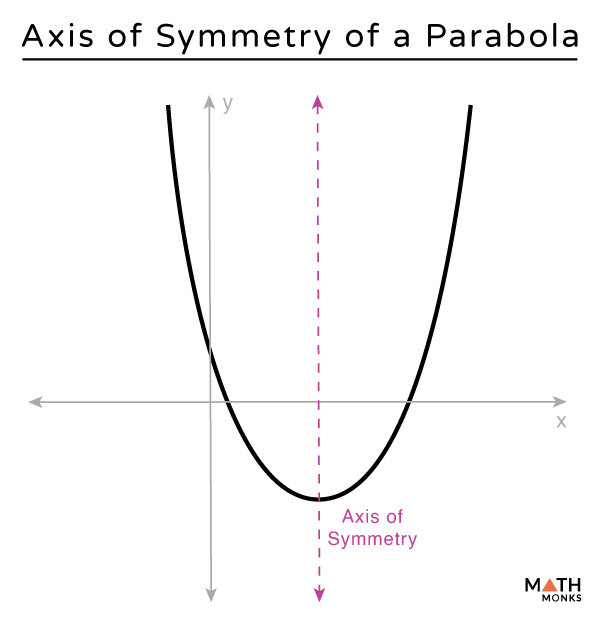
Axis of Symmetry of a Parabola

The axis of symmetry of a parabola is a vertical line that divides a parabola into two halves. This line passes through the vertex of the parabola, which is the highest or lowest point of the graph, depending on its orientation.

Axis of Symmetry of a Parabola

Note: For a parabola facing upward or downward, the axis of symmetry is a vertical line (one is shown above). However, for those that open to the left or right, it is a horizontal line, as shown.

The axis of symmetry is thus the axis of the parabola.

Equations in Standard Form

For quadratic functions in standard form, the axes of symmetry are:

  • For y = ax2 + bx + c, the axis of symmetry is: ${x=-\dfrac{b}{2a}}$
  • For x = ay2 + by + c, the axis of symmetry is: ${y=-\dfrac{b}{2a}}$

Equations in Vertex Form

When parabolas are in vertex form, the axes of symmetry are:

  • For y = a(x – h)2 + k, the axis of symmetry is: x = h
  • For x = a(y – k)2 + h, the axis of symmetry is: y = k

Derivation

Considering the standard quadratic function y = ax2 + bx + c

Here, the constant term ‘c’ does not affect the parabola; thus, the equation can be written as y = ax2 + bx …..(i)

According to the definition, the axis of symmetry is the midpoint of its two x-intercepts. 

To find the x-intercept, substituting y = 0 in the equation (i), we get

0 = ax2 + bx

⇒ x(ax + b) = 0

⇒ x = 0 and x = ${-\dfrac{b}{2a}}$

Now, the mid-point formula is ${x=\dfrac{\left( x_{1}+x_{2}\right) }{2}}$

⇒ ${x=\dfrac{\left( 0+\left( -\dfrac{b}{a}\right) \right) }{2}}$

⇒ ${x=-\dfrac{b}{2a}}$

This is the equation of the axis of symmetry for parabolas in the standard form y = ax2 + bx + c

Similarly, if the parabola opens horizontally (i.e., left/right), we can get the equation for the axis of symmetry by finding the midpoint of the y-intercepts.

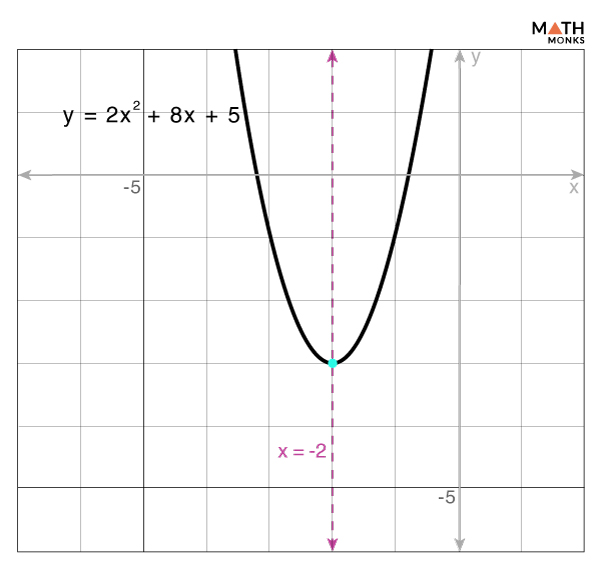
Finding the Axis of Symmetry of the Parabola y = 2x2 + 8x + 5

Given, y = 2x2 + 8x + 5 …..(i)

Comparing the equation (i) of the parabola with the standard form y = ax2 + bx + c, we have

a = 2, b = 8, and c = 5

Using the formula, the axis of symmetry is ${x=-\dfrac{b}{2a}}$ 

⇒ ${x=-\dfrac{8}{2\times 2}}$ 

⇒ ${x=-2}$

Thus, the axis of symmetry is x = -2

By plotting the axis of symmetry of the parabola on the graph, we get

Equation for Axis of Symmetry of Parabola

Solved Examples

Determine the axis of symmetry of the parabola y = 3x2 

Solution:

Given y = 3x2 …..(i)
As we know, the standard form of the parabola is y = ax2 + bx + c …..(ii)
Comparing the equations (i) and (ii), we get
a = 3, b = 0, c = 0
As we know, the axis of symmetry is x = ${-\dfrac{b}{2a}}$
Here, x = ${-\dfrac{0}{2\times 3}}$ 
⇒ x = ${0}$
Thus, the axis of symmetry is x = 0

Find the axis of symmetry of the parabolic function x = y2 – 4y + 3

Solution:

Given x = y2 – 4y + 3 …..(i)
As we know, the standard form of the parabola is x = ay2 + by + c …..(ii)
Comparing the equations (i) and (ii), we get
a = 1, b = -4, and c = 3
As we know, the axis of symmetry is y = ${-\dfrac{b}{2a}}$
Here, y = ${-\dfrac{-4}{2\times 1}}$
⇒ y = ${\dfrac{4}{2}}$
⇒ y = ${2}$
Thus, the axis of symmetry is y = 2

Find the equation of the axis of symmetry for f(x) = -x2 + 4x – 1

Solution:

Given f(x) = -x2 + 4x – 1 …..(i)
As we know, the standard form of the parabola is x = ay2 + by + c …..(ii)
Comparing the equations (i) and (ii), we get
a = -1, b = 4, c = -1
As we know, the axis of symmetry is x = ${-\dfrac{b}{2a}}$ 
Here, x = ${-\dfrac{4}{2\times \left( -1\right) }}$ 
⇒ x = ${2}$
Thus, the axis of symmetry is x = 2

Find the equation of the axis of symmetry for y = 3(x – 5)2 – 4

Solution:

Given y = 3(x – 5)2 – 4 …..(i)
As we know, the vertex form of the parabola is y = a(x – h)2 + k …..(ii)
Comparing the equations (i) and (ii), we get
h = 5 and k = -4
Thus, the axis of symmetry is x = 5

Determine the axis of symmetry of the parabola y = 2(x + 4)2 – 3

Solution:

Given y = 2(x + 4)2 – 3 …..(i)
As we know, the vertex form of the equation of the parabola is y = a(x – h)2 + k …..(ii)
Comparing the equations (i) and (ii), we get
h = 4 and k = -3
Thus, the axis of symmetry is x = 4

Determine the axis of symmetry of the parabola x = 4(y + 3)2 + 1

Solution:

Given x = 4(y + 3)2 + 1 …..(i)
As we know, the vertex form of the parabola is x = a(y – k)2 + h …..(ii)
Comparing the equations (i) and (ii), we get
h = 1 and k = -3
Thus, the axis of symmetry is y = -3

Last modified on November 19th, 2024