A parabola has a distinct ‘U’ shaped curve that represents the graph of a quadratic function y = ax2 + bx + c. Here, a, b, and c are constants, and x is a variable. The shape of the parabolic curve depends on the value of the coefficient a.
- If a > 0, the parabola opens upward
- If a < 0, the parabola opens downward
Domain
The domain of a function is the set of all possible input values (generally represented by x) for which the function is defined. Since a parabola is a polynomial function, it is defined for all real numbers. This means there are no restrictions on the values that x can take. Therefore, the domain of a parabola is written in interval notation as (-∞, ∞). This implies that when we substitute any real number for x in the equation y = ax2 + bx + c, it will give the value of y.
Range
The range of a function is the set of all possible output values (generally represented by y) that the function can produce. Unlike the domain, the range of a parabola depends on its orientation and the position of its vertex.
To determine the range, we need to know the vertex of the parabola and whether it opens upward or downward.
For Parbola that Opens Upwards (a > 0)
- The vertex is the minimum point on the curve
- The range starts at the y-coordinate of the vertex and extends to positive infinity.
If the vertex is at (h, k), then the range is in interval notation as [k, ∞), which means y can take any value greater than or equal to k.
For Parbola that Opens Downwards (a < 0)
- The vertex is the maximum point on the curve
- The range starts from negative infinity and extends to the y-coordinate of the vertex.
If the vertex is at (h, k), then the range is in interval notation as (-∞, k). This indicates that y can take any value less than or equal to k.
How To Find
Let us find the domain and range of the Parabola y = x2 – 4x + 3
Given, y = x2 – 4x + 3 …..(i)
Domain
Since the domain of the quadratic equation is all real values. Thus, the domain is x ∈ (-∞, ∞)
Range
Identifying the Parabola
Since the coefficient of x2 is 1 (positive), the parabola opens upwards.
Finding the Vertex
To find the range, we first complete the square to express the quadratic in the vertex form.
From the equation (i),
y = x2 – 4x + 3
⇒ y = (x2 – 4x + 4) + 3 – 4
⇒ y = (x – 2)2 – 1 …..(ii)
As we know, the equation of the parabola in the vertex form is y = a(x – h)2 + k …..(iii)
Now, comparing the equations (ii) and (iii), we have
h = 2 and k = -1
Thus, the vertex is at (2, -1)
Writing the Range
Thus, the range of the parabola is y ∈ (-1, ∞)
Solved Examples
![]() Determine the domain and range of the parabola given by the equation:
Determine the domain and range of the parabola given by the equation:
y = -2x2 + 8x – 3
Solution:
![]()
Given, y = -2x2 + 8x – 3 …..(i)
Since the domain of the quadratic equation is all real values. Thus, the domain is x ∈ (-∞, ∞)
Since the coefficient of x2 is -2 (negative), the parabola opens downwards.
To find the range, we first complete the square to express the quadratic in the vertex form.
From the equation (i),
y = -2x2 + 8x – 3
⇒ y = -2(x2 – 4x + 4) – 3 + 8
⇒ y = -2(x – 2)2 + 5 …..(ii)
As we know, the equation of the parabola in the vertex form is y = a(x – h)2 + k …..(iii)
Now, comparing the equations (ii) and (iii), we have
h = 2 and k = 5
Thus, the range of the parabola is y ∈ (-∞, 5)
![]() Calculate the domain and range of y = x2 + 6x + 8
Calculate the domain and range of y = x2 + 6x + 8
Solution:
![]()
Given, y = x2 + 6x + 8 …..(i)
Since the domain of the quadratic equation is all real values. Thus, the domain is x ∈ (-∞, ∞)
Since the coefficient of x2 is 1 (positive), the parabola opens upwards.
To find the range, we first complete the square to express the quadratic in the vertex form.
From the equation (i),
y = x2 + 6x + 8
⇒ y = (x2 + 6x + 9) + 8 – 9
⇒ y = (x + 3)2 – 1 …..(ii)
As we know, the equation of the parabola in the vertex form is y = a(x – h)2 + k …..(iii)
Now, comparing the equations (ii) and (iii), we have
h = -3 and k = -1
Thus, the range of the parabola is y ∈ (-1, ∞)
![]() Find the domain and range of the parabola y = -x2 – 4x – 1
Find the domain and range of the parabola y = -x2 – 4x – 1
Solution:
![]()
Given, y = -x2 – 4x – 1 …..(i)
Since the domain of the quadratic equation is all real values. Thus, the domain is x ∈ (-∞, ∞)
Since the coefficient of x2 is -1 (negative), the parabola opens downwards.
To find the range, we first complete the square to express the quadratic in the vertex form.
From the equation (i),
y = -x2 – 4x – 1
⇒ y = -(x2 + 4x + 4) – 1 + 4
⇒ y = -(x + 2)2 + 3 …..(ii)
As we know, the equation of the parabola in the vertex form is y = a(x – h)2 + k …..(iii)
Now, comparing the equations (ii) and (iii), we have
h = -2 and k = 3
Thus, the range of the parabola is y ∈ (-∞, 3)
![]() What is the domain and range of the function y = (x – 2)2 + 3?
What is the domain and range of the function y = (x – 2)2 + 3?
Solution:
![]()
Given, y = (x – 2)2 + 3 …..(i)
The domain is x ∈ (-∞, ∞)
As we know, the equation of the parabola in the vertex form is y = a(x – h)2 + k …..(ii)
Comparing the equations (i) and (ii), we have
a = 1 (> 0), indicating the parabola opens upwards. Also, h = 2 and k = 3
Thus, the range of the parabola is y ∈ (3, ∞)
Problem – Finding the domain and range from the GRAPH OF A PARABOLA
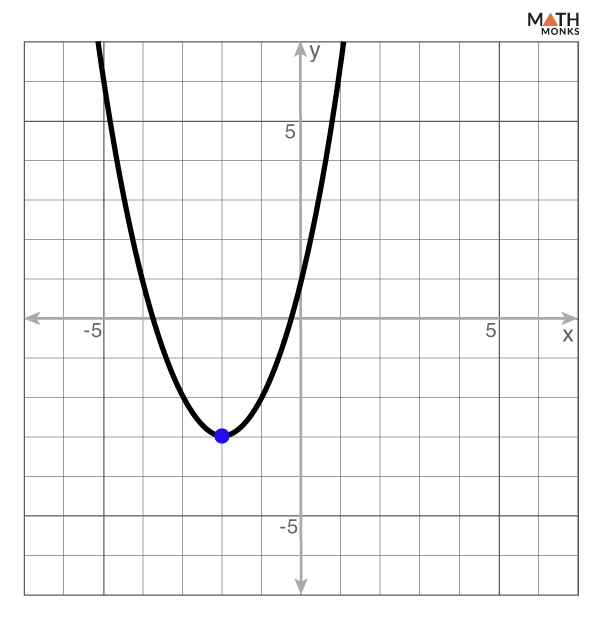 Find the domain and range of the parabola graphed below.
Find the domain and range of the parabola graphed below.
Solution:
![]()
Here, the parabola opens upwards in the graph, and its vertex is at (-2, -3)
Thus, the domain is x ∈ (-∞, ∞) and the range is y ∈ (-3, ∞)
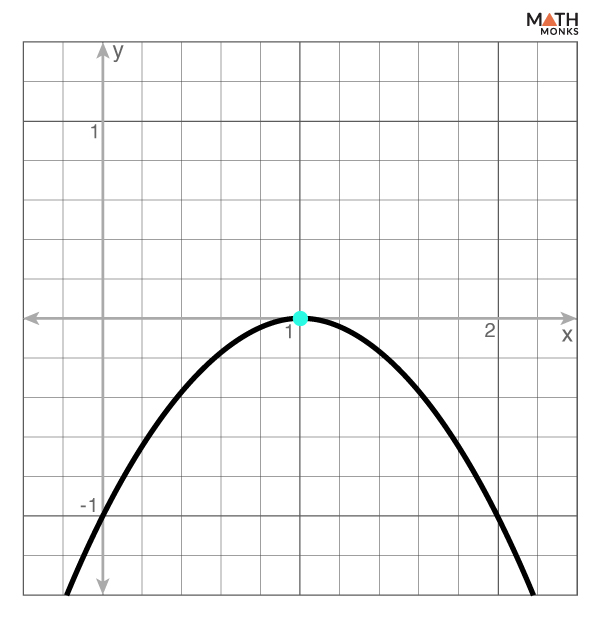 Find the domain and range of the parabola graphed below.
Find the domain and range of the parabola graphed below.
Solution:
![]()
Here, the parabola opens downwards in the graph, and its vertex is at (1, 0)
Thus, the domain is x ∈ (-∞, ∞) and the range is y ∈ (-∞, 0)

 Find the domain and range of the parabola graphed below.
Find the domain and range of the parabola graphed below. Find the domain and range of the parabola graphed below.
Find the domain and range of the parabola graphed below.