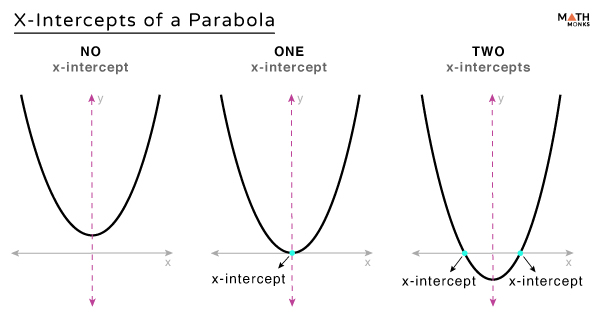
The x-intercepts of a parabola are the points where the U-shaped curve intersects the x-axis. A parabola can have 0, 1, or 2 x-intercepts, as shown.
If a parabola has 1 x-intercept, the x-axis is said to be the tangent to the parabola.
At any x-intercept, the value of y is always 0. The x and y values can be obtained by solving the quadratic function y = ax2 + bx + c, where the discriminant b2 – 4ac determines the nature of the roots.
Finding the Number of X-Intercept(s)
To find the number of x-intercepts for the general quadratic function y = ax2 + bx + c:
- If the discriminant b2 – 4ac < 0, the number of x-intercepts is 0
- If the discriminant b2 – 4ac = 0, the number of x-intercepts is 1
- If the discriminant b2 – 4ac > 0, the number of x-intercepts is 2
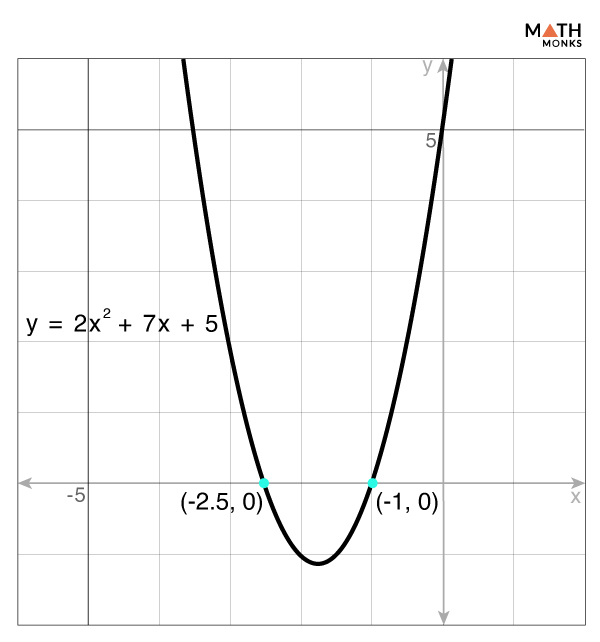
Let us find the number of x-intercepts of the parabola y = 2x2 + 7x + 5
Given, y = 2x2 + 7x + 5 …..(i)
Comparing the equation (i) of the parabola with the standard form y = ax2 + bx + c, we have
a = 2, b = 7, and c = 5
Now, the discriminant is b2 – 4ac = 72 – 4 × 2 × 5 = 9 > 0
Here, b2 – 4ac > 0, and thus, the number of x-intercepts is 2
Finding the X-intercept(s)
The x-intercepts of a parabola determine the roots of its equation and identify the points where the parabola intersects the x-axis. To find the x-intercept(s), we follow the following steps:
- Setting y = 0 in the equation of the parabola
- Solving for x either by factoring or quadratic formula: ${x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$
- Writing the roots in the coordinate form (x, 0)
Let us find the x-intercepts of the parabola y = 2x2 + 7x + 5
Setting y = 0
2x2 + 7x + 5 = 0
Solving for x
Here, we will solve by factoring
⇒ 2x2 + 5x + 2x + 5 = 0
⇒ x(2x + 5) + (2x + 5) = 0
⇒ (2x + 5)(x + 1) = 0
Here, (x + 1) = 0 ⇒ x = -1
(2x + 5) = 0 ⇒ x = ${-\dfrac{5}{2}}$ = -2.5
Writing x in the Coordinate Form
Thus, the x-intercepts (roots) are (-2.5, 0) and (-1, 0)
Plotting the given parabola in the graph, we get the x-intercepts, as shown.
![]() Find the x-intercepts of the parabola represented by the equation: y = x2 – 4x – 5
Find the x-intercepts of the parabola represented by the equation: y = x2 – 4x – 5
Solution:
![]()
Given, y = x2 – 4x – 5 …..(i)
Considering y = 0 in the equation (i), we get
x2 – 4x – 5 = 0
⇒ x2 – 5x + x – 5 = 0
⇒ x(x – 5) + (x – 5) = 0
⇒ (x + 1)(x – 5) = 0
Now, (x + 1) = 0 ⇒ x = -1
(x – 5) = 0 ⇒ x = 5
Thus, the x-intercepts are (-1, 0) and (5, 0)
![]() Determine the x-intercepts of the parabola y = 2x2 – 6x + 4 using the quadratic root formula
Determine the x-intercepts of the parabola y = 2x2 – 6x + 4 using the quadratic root formula
Solution:
![]()
Given, y = 2x2 – 6x + 4 …..(i)
As we know, the standard form of the parabola is y = ax2 + bx + c …..(ii)
Comparing the equations (i) and (ii), we have
a = 2, b = -6, c = 4
Now, setting y = 0, we get
2x2 – 6x + 4 = 0
⇒ ${x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$
⇒ ${x=\dfrac{-\left( -6\right) \pm \sqrt{\left( -6\right) ^{2}-4\times 2\times 4}}{2\times 2}}$
⇒ x = 2 and x = 1
Thus, the x-intercepts are (2, 0) and (1, 0)
Problem – Finding the x-intercept of a parabola with a SINGLE INTERCEPT
![]() Find the x-intercepts of the parabola y = x2 + 2x + 1
Find the x-intercepts of the parabola y = x2 + 2x + 1
Solution:
![]()
Given, y = x2 + 2x + 1 …..(i)
As we know, the standard form of the parabola is y = ax2 + bx + c …..(ii)
Comparing the equations (i) and (ii), we have
a = 1, b = 2, and c = 1
Here, the discriminant is b2 – 4ac = (2)2 – 4(1)(1) = 0
Thus, the parabola has 1 x-intercept.
Considering y = 0, we get
x2 + 2x + 1 = 0
⇒ (x + 1)2 = 0
⇒ (x + 1) = 0
⇒ x = -1
Thus, the x-intercept is (-1, 0)
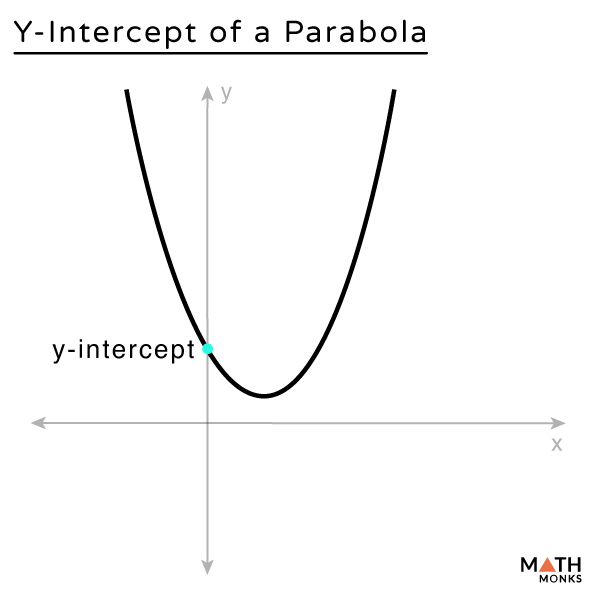
Finding the Y-Intercept
Like x-intercepts, each parabola contains a y-intercept, the point at which the parabola intercepts the y-axis.
To find the y-intercept, we follow the following steps:
- Setting x = 0 in the equation
- Solving for y
- Writing y in the coordinate form (0, y)
Now, let us find the y-intercepts of the parabola y = 2x2 + 7x + 5
Setting x = 0
y = 2(0)2 + 7(0) + 5
Solving for y
⇒ y = 5
Writing y in the coordinate form
Thus, the y-intercept is (0, 5)
Plotting the given parabola on the graph, we get the y-intercept, as shown.
![]() Determine the x and y-intercepts of the following parabola:
Determine the x and y-intercepts of the following parabola:
y = 2x2 + 3x – 5
Solution:
![]()
Given, y = 2x2 + 3x – 5 …..(i)
Considering y = 0 in the equation (i), we get
2x2 + 3x – 5 = 0
⇒ 2x2 + 5x – 2x – 5 = 0
⇒ x(2x + 5) – (2x + 5) = 0
⇒ (2x + 5)(x – 1) = 0
Now, (2x + 5) = 0 ⇒ x = ${-\dfrac{5}{2}}$ = -2.5
(x – 1) = 0 ⇒ x = 1
Thus, the x-intercepts are (-2.5, 0) and (1, 0)
By putting x = 0 in the equation (i), we get
y = 2(0)2 + 3(0) – 5
⇒ y = -5
Thus, the y-intercept is (0, -5)
![]() Find the x and y-intercepts of y = 4x2 – 8x
Find the x and y-intercepts of y = 4x2 – 8x
Solution:
![]()
Given, y = 4x2 – 8x …..(i)
Considering y = 0 in the equation (i), we get
4x2 – 8x = 0
⇒ 4x(x – 2) = 0
Now, 4x = 0 ⇒ x = 0
(x – 2) = 0 ⇒ x = 2
Thus, the x-intercepts are (0, 0) and (2, 0)
By putting x= 0 in the equation (i), we get
y = 4(0)2 – 8(0)
⇒ y = 0
Thus, the y-intercept is (0, 0)
![]() Find the x and y-intercepts of the parabola y = 5x2 + 15x + 10
Find the x and y-intercepts of the parabola y = 5x2 + 15x + 10
Solution:
![]()
Given, y = 5x2 + 15x + 10 …..(i)
Considering y = 0 in the equation (i), we get
5x2 + 15x + 10 = 0
⇒ x2 + 3x + 2 = 0
⇒ x2 + 2x + x + 2 = 0
⇒ x(x + 2) + (x + 2) = 0
⇒ (x + 2)(x + 1) = 0
Now, (x + 2) = 0 ⇒ x = -2
(x + 1) = 0 ⇒ x = -1
Thus, the x-intercepts are (-2, 0) and (-1, 0)
By putting x = 0 in the equation (i), we get
y = 5(0)2 + 15(0) + 10
⇒ y = 10
Thus, the y-intercept is (10, 0)
Problem – Finding X & Y INTERCEPTS of a parabola given in VERTEX FORM
![]() Determine the x and y intercepts of the parabola y = 2(x – 2)2 – 3
Determine the x and y intercepts of the parabola y = 2(x – 2)2 – 3
Solution:
![]()
Given, y = 2(x – 2)2 – 3 …..(i)
Considering y = 0 in the equation (i), we get
2(x – 2)2 – 3 = 0
⇒ 2(x2 – 4x + 4) – 3 = 0
⇒ 2x2 – 8x + 8 – 3 = 0
⇒ 2x2 – 8x + 5 = 0 …..(ii)
As we know, the standard form of the parabola is y = ax2 + bx + c …..(iii)
Comparing the equations (ii) and (iii), we have
a = 2, b = -8, c = 5
Here, ${x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$
⇒ ${x=\dfrac{-\left( -8\right) \pm \sqrt{\left( -8\right) ^{2}-4\times 2\times 5}}{2\times 2}}$
⇒ x = ${2+\sqrt{\dfrac{3}{2}}}$ and x = ${2-\sqrt{\dfrac{3}{2}}}$
Thus, the x-intercepts are ${\left( 2+\sqrt{\dfrac{3}{2}},0\right)}$ and ${\left( 2-\sqrt{\dfrac{3}{2}},0\right)}$
By putting x = 0 in the equation (i), we get
y = 2(0 – 2)2 – 3 = 8 – 3 = 5
⇒ y = 5
Thus, the y-intercept is (0, 5)