A parabola is a graph of a quadratic function that can be expressed in two forms:
- General Form: y = ax2 + bx + c
- Vertex Form: y = a(x – h)2 + k
The vertex form is particularly used for transformations as it indicates the orientation of the curve. There are four main types of transformations: translation (shifting), stretching or compressing, reflection, and rotation.
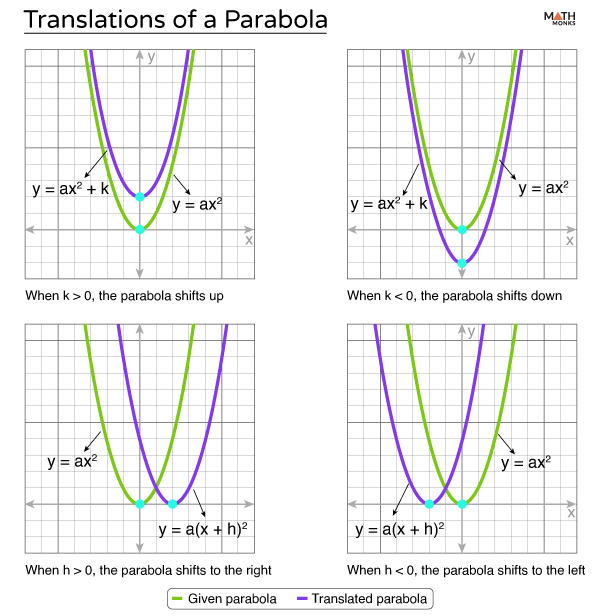
Translation
Translations move the parabola up, down, left, or right without changing its shape.
Vertical
For a parabolic function of the form y = ax2, vertical translation shifts the graph up or down by adding or subtracting a constant to the equation. The translated equation becomes y = ax2 + k
- If k is positive (> 0), the parabola moves upwards
- If k is negative (< 0), it moves downwards
Horizontal
Similarly, horizontal translation shifts the graph to the left or right by adding or subtracting a constant to the x-variable in the equation. The translated equation becomes y = a(x – h)2
- If h is positive (> 0), the parabola moves to the right
- If h is negative (< 0), it moves to the left
![]()
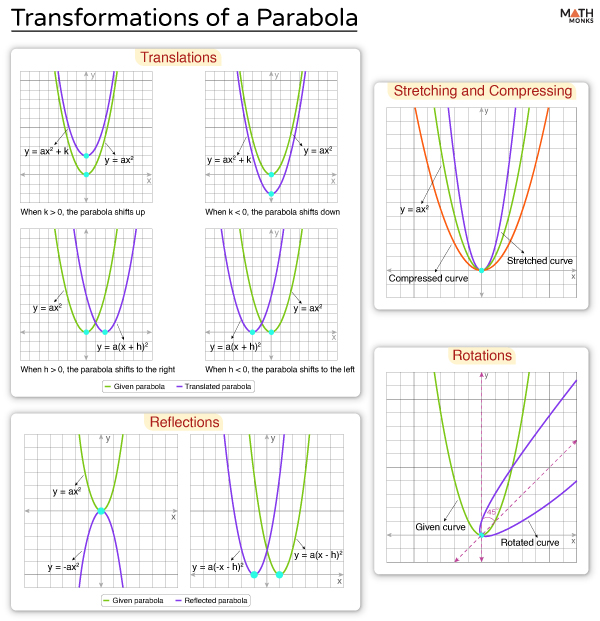
Sketch the transformed parabola of y = x2 when it is translated 4 units up.
Solution:
Given parabola is of the form y = x2 …..(i)
As we know, if the graph y = ax2 is vertically translated for k units up, it becomes y = ax2 + k (k > 0)
Now, translating the equation (i) 4 units up, we get
y = x2 + 4
When plotting the resulting parabola, we obtain the graph shown.
![]()
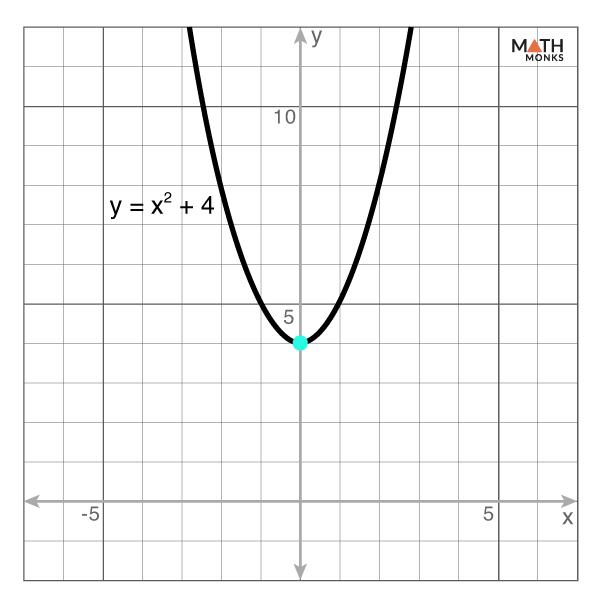
Graph the transformed parabola of y = x2 when it is translated 7 units to the left.
Solution:
Given parabola is of the form y = x2 …..(i)
As we know, if the graph y = ax2 is vertically translated for h units to the left, it becomes y = a(x – h)2 (h < 0)
Now, translating the equation (i) 7 units to the left, we get
y = (x + 7)2
When plotting the resulting parabola, we obtain the graph shown.
The translated parabola will have its vertex at (h, k) and is congruent to the original parabola.
For y = ax2, the translated equation is y = a(x – h)2 + k
If h > 0, the parabola shifts to the right; if h < 0, it shifts to the left
If k > 0, the parabola shifts up; if k < 0, it shifts down
![]()
Given the equation, y = (x – 4)2 + 3, find the transformation that has occurred compared to y = x2
Solution:
![]()
Given y = (x – 4)2 + 3 …..(i)
Here, equation (i) is a transformation of the parent function y = x2
As we know, the parent function y = x2 represents a parabola with its vertex at (0, 0)
Since its translated equation is y = (x – h)2 + k …..(ii)
Comparing the equations (i) and (ii), we get
h = 4 (> 0) and k = 3 (> 0)
Thus, the graph of the equation y = (x – 4)2 + 3 is shifted 4 units to the right and 3 units up from the origin (0, 0)
![]()
If the equation of a transformed parabola is y = (x + 3)2 – 2, find how the vertex has moved from the origin and write the coordinates of the new vertex.
Solution:
![]()
Given y = (x + 3)2 – 2 …..(i)
Here, equation (i) is a transformation of the parent function y = x2
As we know, the parent function y = x2 represents a parabola with its vertex at (0, 0)
Since its translated equation is y = (x – h)2 + k …..(ii)
Comparing the equations (i) and (ii), we get
h = -3 (< 0) and k = -2 (< 0)
Thus, the graph of the equation y = (x + 3)2 – 2 is shifted 3 units to the left and 2 units down from the origin (0, 0)
The new vertex is at (-3, -2)
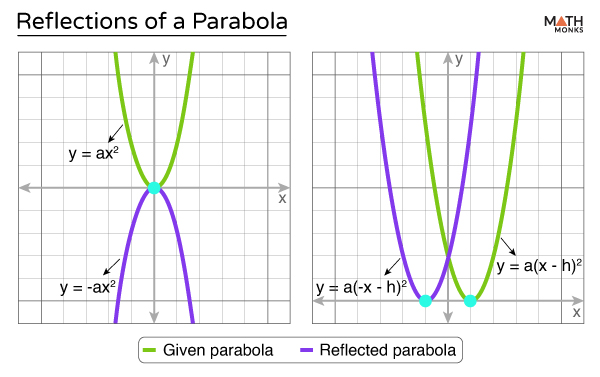
Reflecting
Reflections change the direction in which the parabola opens.
Along X-axis
If the original parabolic function is y = ax2, then reflecting across the x-axis changes the equation to:
y = -ax2
Here, a parabola that opens upwards (when a > 0) becomes a parabola that opens downwards (when a < 0) or vice versa.
Along Y-axis
If the original parabolic function is y = ax2, then reflecting across the y-axis changes the equation to:
y = a(-x)2, flipping the parabola horizontally.
![]()
Given the parabola y = 4x2 – 7, what is the resulting equation if a reflection is done across both the x-axis and the y-axis?
Solution:
![]()
Given, y = 4x2 – 7 …..(i)
As we know, if the parabola y = ax2 is reflected across the x-axis, then its equation becomes y = -ax2
Also, if the parabola y = ax2 is reflected across the y-axis, its equation becomes y = a(-x)2
Thus, if the equation (i) is reflected across both the x-axis and y-axis, the equation of the reflected parabola is
y = -4x2 – 7
![]()
A parabola with the equation y = (x + 4)2 – 1 is reflected across the y-axis. What is the equation of the reflected parabola? Sketch the new graph.
Solution:
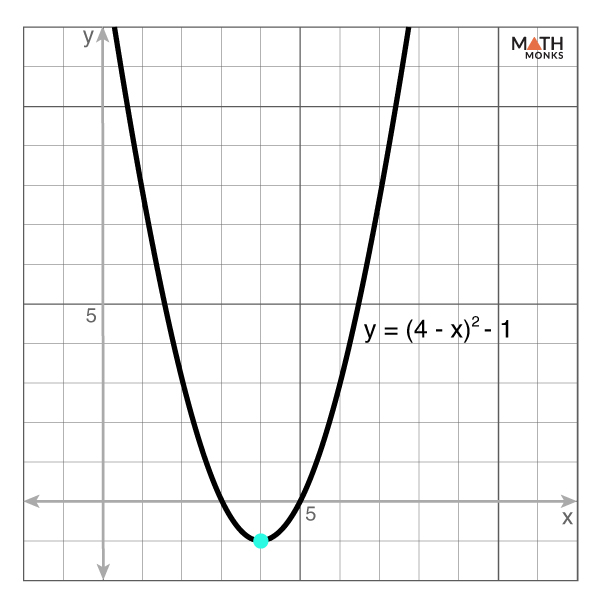
Given, y = (x + 4)2 – 1 …..(i)
As we know, if the parabola y = ax2 is reflected across the y-axis, its equation becomes y = a(-x)2
Here, if the equation (i) is reflected across the y-axis, the equation of the reflected parabola is
y = (-x + 4)2 – 1
⇒ y = (4 – x)2 – 1
Thus, the equation of the reflected parabola is y = (4 – x)2 – 1
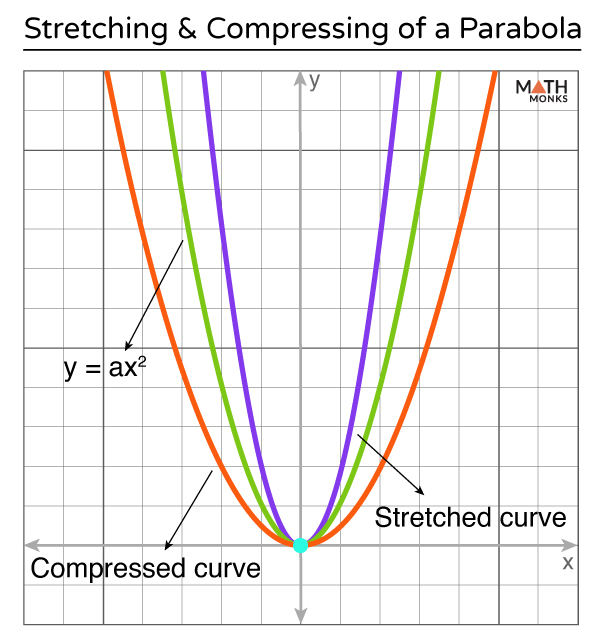
Stretching and Compressing
Stretching or compressing a parabola changes its shape by making it narrower or wider while the vertex remains unchanged. This transformation is determined by the coefficient a of the quadratic term x2 in the parabola equation.
For the equation y = ax2,
- Vertical Stretch: If ∣a∣ > 1, the parabola becomes narrower (stretched vertically), and the curve appears steeper.
- Vertical Compression: If 0 < ∣a∣ < 1, the parabola becomes wider (compressed vertically), and the curve appears flatter.
![]()
Graph the parabola for y = 2x2 and compare it to the graph of y = x2. Describe the transformation.
Solution:
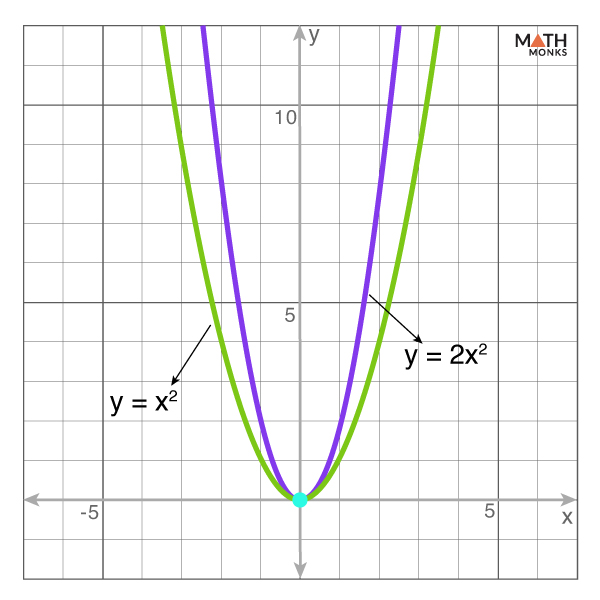
Given, y = 2x2 …..(i)
y = x2 …..(ii)
When comparing equations (i) and (ii), a = the coefficient of x2 in equation (i) is 2 (> 1), representing the parabola (i) is vertically stretched.
The vertex of both parabolas remains at the origin (0,0), but the parabola (i) is stretched upwards, making it steeper compared to the parabola (ii).
![]()
Given the equation y = 2x2 + 12x + 11, describe how the parabola is vertically stretched compared to the standard parabola y = a(x – h)2 + k.
Solution:
![]()
Given y = 2x2 + 12x + 11 …..(i)
⇒ y = 2(x2 + 6x + 9) + 11 – 18
⇒ y = 2(x + 3)2 – 7 …..(ii)
Now, comparing the equation (ii) with the given standard equation, we get
a = 2, h = -3, and k = -7
Since a = 2 (> 1), the parabola is vertically stretched.
Thus, the parabola y = 2x2 + 12x + 11 is vertically stretched by a factor of 2 compared to the equation y = a(x – h)2 + k
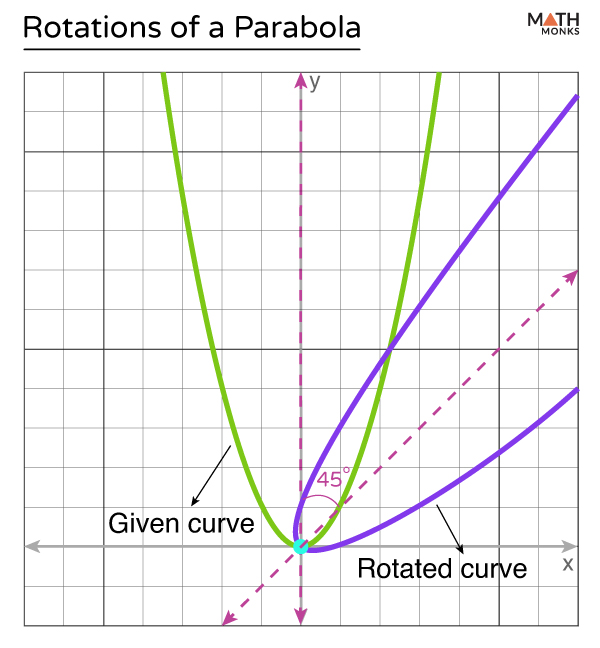
Rotation
A parabola can also be rotated around a specific point, typically the origin, by a certain angle. When this happens, the parabola no longer aligns with the standard axes, and the equation changes to reflect the new orientation.
For example, rotating a parabola clockwise by angles like 45° or 90° about the origin will result in a more complex equation that includes both x2 and xy terms.
Here is a summary of all types of parabola transformations.
