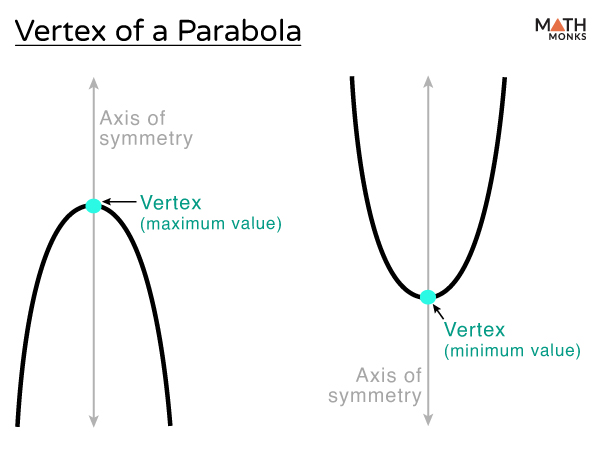
The vertex of a parabola is the point of intersection of the parabola with its line of symmetry. It is the point where the parabola changes its direction and thus is the highest or lowest point on the curve. Every parabola has exactly one vertex, which is represented by (h, k).
For a parabola in the standard form, y = ax2 + bx + c, if the coefficient of x2 (i.e., a) is positive, the parabola opens upwards (forming a ‘U’ shape) and has a minimum value. If the coefficient of x2 (i.e., a) is negative, the parabola opens downwards (forming a ‘⋂’ shape) and has a maximum value.
In contrast, if a parabola opens horizontally to the left or right, the vertex is neither the maximum nor the minimum point.
Formulas
A parabola in standard form:
- f(x) = ax2 + bx + c, has its vertex at ${\left( -\dfrac{b}{2a},f\left( -\dfrac{b}{2a}\right) \right)}$
- f(y) = ay2 + by + c, has its vertex at ${\left( f\left( -\dfrac{b}{2a}\right),-\dfrac{b}{2a} \right)}$
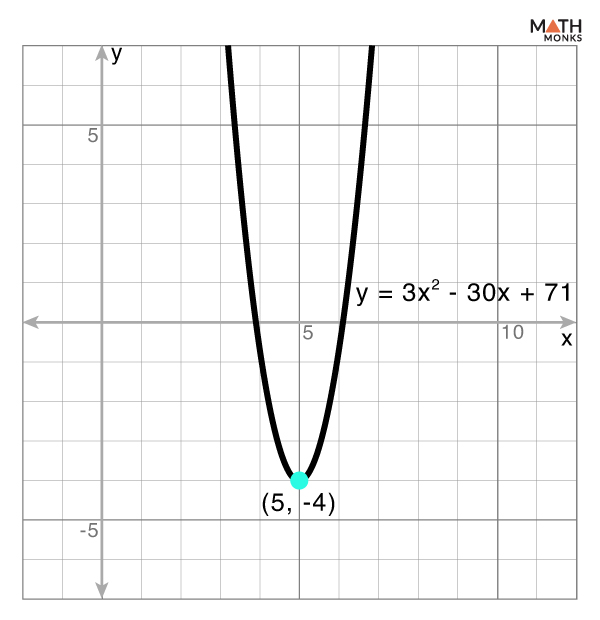
For example, the vertex of the parabola y = 3x2 – 30x + 71 is at (5, -4)
Derivation
Let us consider the parabola y = ax2 + bx + c
Subtracting c from both sides,
⇒ ${y-c=ax^{2}+bx}$
Taking out the common factor (i.e., a) from the right-hand side,
⇒ ${y-c=a\left( x^{2}+\dfrac{bx}{a}\right)}$
Adding and subtracting ${\dfrac{b^{2}}{4a^{2}}}$ on the right-hand side,
⇒ ${y-c=a\left( x^{2}+\dfrac{b}{a}x+\dfrac{b^{2}}{4a^{2}}-\dfrac{b^{2}}{4a^{2}}\right)}$
⇒ ${y-c=a\left( \left( x+\dfrac{b}{2a}\right) ^{2}-\dfrac{b^{2}}{4a^{2}}\right)}$
⇒ ${y-c=a\left( x+\dfrac{b}{2a}\right) ^{2}-\dfrac{b^{2}}{4a}}$
⇒ ${y=a\left( x+\dfrac{b}{2a}\right) ^{2}-\dfrac{b^{2}}{4a}+c}$
⇒ ${y=a\left( x+\dfrac{b}{2a}\right) ^{2}-\left( \dfrac{b^{2}}{4a}-c\right)}$
⇒ ${y=a\left( x+\dfrac{b}{2a}\right) ^{2}-\left( \dfrac{b^{2}-4ac}{4a}\right)}$
Since b2 – 4ac is discriminant (say, D) of the standard equation as y = ax2 + bx + c
⇒ ${y=a\left( x+\dfrac{b}{2a}\right) ^{2}-\dfrac{D}{4a}}$ …..(i)
Since a parabola in the vertex form, y = a(x – h)2 + k, has its vertex at (h, k) …..(ii)
Now, comparing the equations (i) and (ii), we get
h = ${-\dfrac{b}{2a}}$ and k = ${-\dfrac{D}{4a}}$
Thus, the vertex is ${\left( -\dfrac{b}{2a},-\dfrac{D}{4a}\right)}$
Similarly, we can get the vertex of the parabola x = ay2 + by + c at ${\left( f\left( -\dfrac{b}{2a}\right),-\dfrac{b}{2a} \right)}$
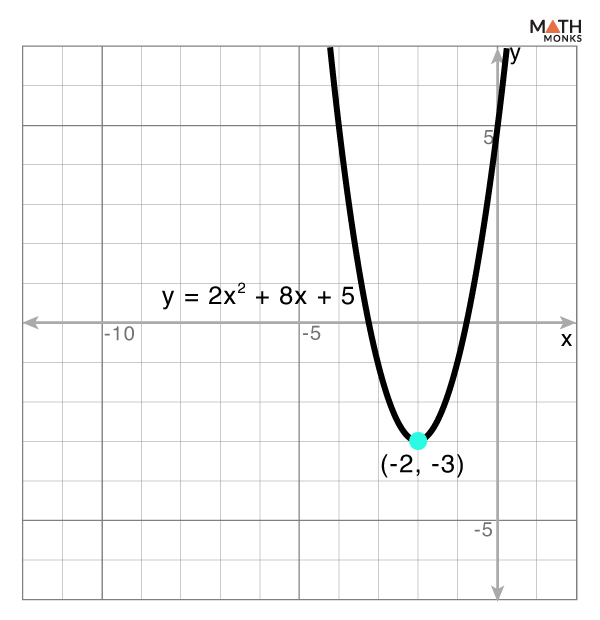
Finding the Vertex of the Parabola y = 2x2 + 8x + 5
Given, y = 2x2 + 8x + 5 …..(i)
Comparing the equation (i) of the parabola with the standard form y = ax2 + bx + c, we have
a = 2, b = 8, and c = 5
Using the formula, the x-coordinate of the vertex is h = ${-\dfrac{b}{2a}}$
⇒ h = ${-\dfrac{8}{2\times 2}}$
⇒ h = ${-2}$
Now, substituting x = h in the equation (i), we get
k = f(h) = 2(-2)2 + 8(-2) + 5
⇒ k = 8 – 16 + 5
⇒ k = -3
Thus, the vertex is (h, k) = (-2, -3)
By plotting the vertex of the parabola on the graph, we get
Solved Examples
![]()
Find the vertex of the parabolic function x = y2 – 4y + 3
Solution:
![]()
Given x = y2 – 4y + 3 …..(i)
As we know, the standard form of the parabola is x = ay2 + by + c …..(ii)
Comparing the equations (i) and (ii), we get
a = 1, b = -4, and c = 3
As we know, the x-coordinates of the vertex is h = ${-\dfrac{b}{2a}}$
Here, h = ${-\dfrac{-4}{2\times 1}}$
⇒ h = ${\dfrac{4}{2}}$
⇒ h = ${2}$
Substituting x = h in the equation (i), we get
k = f(h) = (2)2 – 4(2) + 3
⇒ k = 4 – 8 + 3
⇒ k = -1
Thus, the vertex is (h, k) = (2, -1)
![]()
Identify the vertex of y = 3(x – 5)2 – 4
Solution:
![]()
Given y = 3(x – 5)2 – 4 …..(i)
As we know, the vertex form of the parabola is y = a(x – h)2 + k …..(ii)
Comparing the equations (i) and (ii), we get
h = 5 and k = -4
Thus, the vertex (h, k) as an ordered pair is (5, -4)
![]()
Determine the vertex of the parabola y = 2(x + 4)2 – 3
Solution:
![]()
Given y = 2(x + 4)2 – 3 …..(i)
As we know, the vertex form of the equation of the parabola is y = a(x – h)2 + k …..(ii)
Comparing the equations (i) and (ii), we get
h = 4 and k = -3
Thus, the vertex of the parabola is at (4, -3)
![]()
Determine the vertex of the parabola x = 4(y + 3)2 + 1
Solution:
![]()
Given x = 4(y + 3)2 + 1 …..(i)
As we know, the vertex form of the parabola is x = a(y – k)2 + h …..(ii)
Comparing the equations (i) and (ii), we get
h = 1 and k = -3
Thus, the vertex is (h, k) = (1, -3)
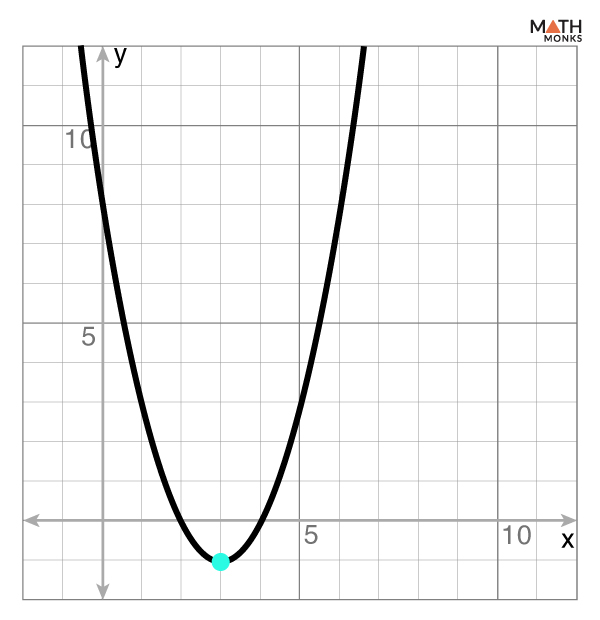What is the vertex of the parabola in the graph?
Solution:
![]()
The given graph shows a parabola that opens upwards.
Here, the axis of symmetry is x = 3, which cuts the parabola at (3, -1)
As we know, the intersection point of the parabola and its axis of symmetry is called the vertex.
Thus, the vertex is (3, -1)
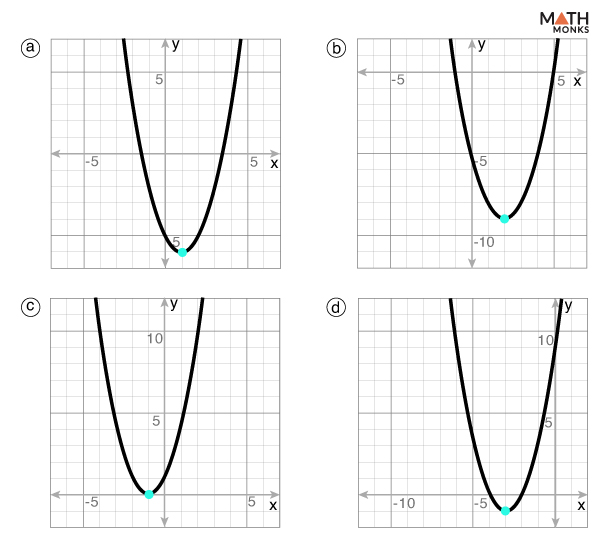Which parabola will have a minimum value vertex?
Solution:
![]()
Here, the vertices and the y-coordinates are
a) (1, -6) and k = -6
b) (2, -9) and k = -9
c) (-1, 0) and k = 0
d) (-3, -1) and k = -1
Thus, option b) has the minimum value vertex.
Problem: Finding the vertex when the parabola is given in the INTERCEPT FORM
If the equation of a parabola is given in the intercept form y = a(x – p)(x – q), then the vertex is at ${\left( \dfrac{p+q}{2},f\left( \dfrac{p+q}{2}\right) \right)}$, here(p, 0) and (q, 0) are the x-intercepts of the parabola.
If the equation of the parabola is in the form x = a(y – p)(y – q), then the vertex is at ${\left( f\left( \dfrac{p+q}{2}\right) ,\dfrac{p+q}{2}\right)}$, here (p, 0) and (q, 0) are the y-intercepts of the parabola
![]()
Determine the vertex of y = -2(x – 3)(x + 4)
Solution:
![]()
Given y = -2(x – 3)(x + 4) …..(i)
As we know, the intercept form of the parabola is y = a(x – p)(x – q) …..(ii)
Comparing the equations (i) and (ii), we get
p = 3 and q = -4
Using the formula, the x-coordinate of the vertex is h = ${\dfrac{p+q}{2}}$
⇒ h = ${\dfrac{3-4}{2}}$
⇒ h = ${-\dfrac{1}{2}}$
Now, substituting x = h in the equation (i), we get
k = ${f\left( \dfrac{p+q}{2}\right)}$
⇒ k = ${f\left( -\dfrac{1}{2}\right)}$
⇒ k = ${-2\left( -\dfrac{1}{2}-3\right) \left( -\dfrac{1}{2}+4\right)}$
⇒ k = ${-2\left( \dfrac{-1-6}{2}\right) \left( \dfrac{-1+8}{2}\right)}$
⇒ k = ${-2\left( \dfrac{-7}{2}\right) \left( \dfrac{7}{2}\right)}$
⇒ k = ${\dfrac{49}{2}}$
Thus, the vertex (h, k) as an ordered pair is ${\left( -\dfrac{1}{2},\dfrac{49}{2}\right)}$
![]()
Find the vertex of x = (y – 2)(y + 8)
Solution:
![]()
Given x = (y + 2)(y – 8) …..(i)
As we know, the intercept form of the parabola is x = a(y – p)(y – q) …..(ii)
Comparing the equations (i) and (ii), we get
p = -2 and q = 8
Using the formula, the y-coordinate of the vertex is k = ${\dfrac{p+q}{2}}$
⇒ k = ${\dfrac{-2+8}{2}}$
⇒ k = ${\dfrac{6}{2}}$
⇒ k = ${3}$
Now, substituting y = k in the equation (i), we get
h = ${f\left( \dfrac{p+q}{2}\right)}$
⇒ h = f(3)
⇒ h = (3 – 2)(3 + 8)
⇒ h = 11
Thus, the vertex is (h, k) = (11, 3)
