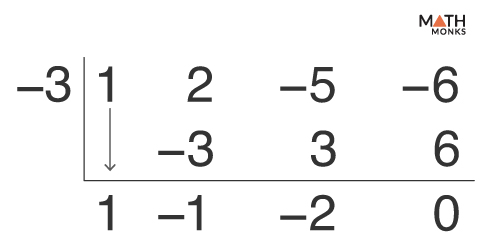A cubic polynomial is a type of polynomial in which the highest power of the variable, or degree, is 3. It typically has up to four terms.
Here are a few examples of cubic polynomials:
- 2x3 + 5x2 + 3x + 4
- -x3 + 6x2 + x – 1
- x3 + 1
Formula
The general form of a cubic polynomial is:
ax3 + bx2 + cx + d
Here,
- x is a variable
- a, b, c, and d are real numbers
- a ≠ 0
Thus, the cubic polynomial equation takes the form ax3 + bx2 + cx + d = 0. The values of x that satisfy the cubic equation are called the roots or zeros of the cubic polynomial.
Finding Zeros or Roots
Let us find the zeros of the cubic equation x3 – 6x2 + 11x = 6
Arranging in the Standard Form
x3 – 6x2 + 11x = 6
⇒ x3 – 6x2 + 11x – 6 = 0
Breaking Down to the Product of Linear and Quadratic Factors
⇒ x3 – x2 – 5x2 + 5x + 6x – 6 = 0
⇒ x2(x – 1) – 5x(x – 1) + 6(x – 1) = 0
⇒ (x – 1)(x2 – 5x + 6) = 0 …..(i)
Solving the Quadratic Factor
⇒ (x – 1)(x2 – 3x – 2x + 6) = 0
⇒ (x – 1)[x(x – 3) – 2(x – 3)] = 0
⇒ (x – 1)(x – 3)(x – 2) = 0 …..(ii)
Solving for x
Now, from (ii), we get
(x – 1) = 0 ⇒ x = 1
(x – 2) = 0 ⇒ x = 2
(x – 3) = 0 ⇒ x = 3
Thus, the roots or zeros are x = 1, 2, and 3
A cubic polynomial of the form of P(x) = ax3 + bx2 + cx + d (a ≠ 0) typically has 3 roots.
Alternate Method: Using Formulas
If the roots of a cubic polynomial are p, q, and r, they satisfy these relations:
- ${p+q+r=-\dfrac{b}{a}}$
- ${pq+qr+rp=\dfrac{c}{a}}$
- ${pqr=-\dfrac{d}{a}}$
Let us find the roots of x3 – 6x2 + 11x = 6 using formulas, assuming the roots are in arithmetic progression.
Since the roots are in arithmetic progression, the roots p, q, and r are x – d, x, and x + d, respectively.
Finding the Linear Factor
From the equation, we get
x3 – 6x2 + 11x = 6
⇒ x3 – 6x2 + 11x – 6 = 0 …..(i)
Now, comparing equation (i) with the standard form of the cubic equation, we get
a = 1, b = -6, c = 11, and d = -6
Using the cubic formula for the sum of roots, we get
${p+q+r=-\dfrac{b}{a}}$
⇒ ${x-d+x+x+d=-\dfrac{\left( -6\right) }{1}}$
⇒ 3x = 6
⇒ x = ${\dfrac{6}{3}}$
⇒ x = 2 …..(ii)
Thus, x = 2 is one of the roots. We can find the other roots by factoring the cubic equation into a quadratic equation.
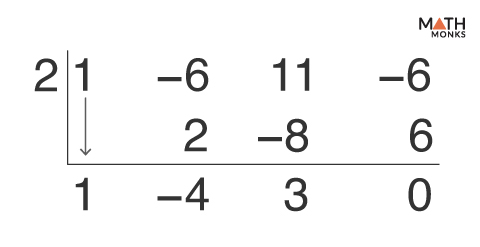
Finding Other Factors by Synthetic Division
By factoring a cubic polynomial, we get simpler polynomials whose product gives the original function. Each simpler polynomial is a factor of the cubic polynomial.
According to the factor theorem, (x – a) is a factor of the polynomial P(x) of degree n ≥ 1 if and only if P(a) = 0, where a is any real number.
The formula of the factor theorem is given by P(x) = (x – a) Q(x)
If P(x) is a cubic polynomial, then Q(x) is a quadratic polynomial. Now, using synthetic division, we can divide P(x) by (x – a) to find the factors of P(x).
Now, when factoring x3 – 6x2 + 11x – 6 = 0 with (x – 2) as one of the factors, we can find the other factor Q(x) by synthetic division.
Here, the quotient Q(x) is x2 – 4x + 3 (one order less than the given polynomial), and the remainder is 0
Thus, x3 – 6x2 + 11x – 6 is factored as (x – 2)(x2 – 4x + 3) …..(iii)
Factoring the Quadratic Quotient
Now, Q(x) can further be factored by the quadratic formula.
x = ${\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$
⇒ x = ${\dfrac{-\left( -4\right) \pm \sqrt{\left( -4\right) ^{2}-4\times 1\times 3}}{2\times 1}}$
⇒ x = ${\dfrac{4\pm \sqrt{16-12}}{2}}$
⇒ x = ${\dfrac{4\pm \sqrt{4}}{2}}$
⇒ x = ${\dfrac{4\pm 2}{2}}$
⇒ x = 3 and 1 …..(iv)
Thus, from (ii) and (iv), we get
x = 1, 2, and 3 are the roots of x3 – 6x2 + 11x = 6
The quadratic part can also be factored by the middle-term method.
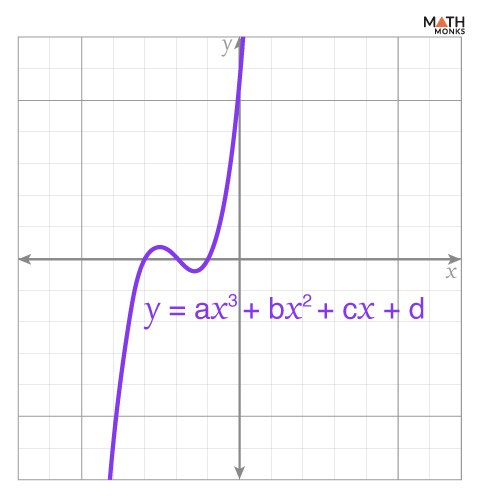
Graphing
When a cubic polynomial cannot be solved using the methods mentioned above, it can be solved graphically. The points where the graph intersects the x-axis (x-intercepts) represent the solutions, also known as the roots of the cubic polynomial.
While plotting a graph for a cubic polynomial:
- If the coefficient of x3 (denoted by ‘a’) is positive, the graph will extend from down to up.
- If the coefficient of x3 (denoted by ‘a’) is negative, the graph will extend from up to down.
A general cubic polynomial graph is shown:
Solved Examples
![]() Solve the cubic equation x3 + 2x2 – 5x – 6 = 0 by factoring.
Solve the cubic equation x3 + 2x2 – 5x – 6 = 0 by factoring.
Solution:
![]()
Given, x3 + 2x2 – 5x – 6 = 0
⇒ x3 – 2x2 + 4x2 – 8x + 3x – 6 = 0
⇒ x2(x – 2) + 4x(x – 2) + 3(x – 2) = 0
⇒ (x – 2)(x2 + 4x + 3) = 0
⇒ (x – 2)(x2 + 3x + x + 3) = 0
⇒ (x – 2)[x(x + 3) + 1(x + 3)] = 0
⇒ (x – 2)(x + 3 )(x + 1) = 0
Here,
(x – 2) = 0 ⇒ x = 2
(x + 3) = 0 ⇒ x = -3
(x + 1) = 0 ⇒ x = -1
Thus, x = -1, -3, and 2 are the solutions of the cubic equation x3 + 2x2 – 5x – 6 = 0
![]() Express g(x) = 2x3 + 5x2 – 4x – 12 as a product of linear and quadratic factors.
Express g(x) = 2x3 + 5x2 – 4x – 12 as a product of linear and quadratic factors.
Solution:
![]()
Given, 2x3 + 5x2 – 4x – 12
= 2x3 + 4x2 + x2 + 2x – 6x – 12
= 2x2(x + 2) + x(x + 2) – 6(x + 2)
= (x + 2)(2x2 + x – 6)
Thus, 2x3 + 5x2 – 4x – 12 = (x + 2)(2x2 + x – 6)
![]() If P(x) = x3 + 4x2 + x – 6, evaluate P(-3)
If P(x) = x3 + 4x2 + x – 6, evaluate P(-3)
Solution:
![]()
Given, P(x) = x3 + 4x2 + x – 6
Now, substituting x = -3, we get
P(-3) = (-3)3 + 4(-3)2 + (-3) – 6
= -27 + 36 – 3 – 6
= 0
Thus, P(-3) = 0
![]() If x = -3 is a root of the polynomial h(x) = x3 + 2x2 – 5x – 6, find the other roots.
If x = -3 is a root of the polynomial h(x) = x3 + 2x2 – 5x – 6, find the other roots.
Solution:
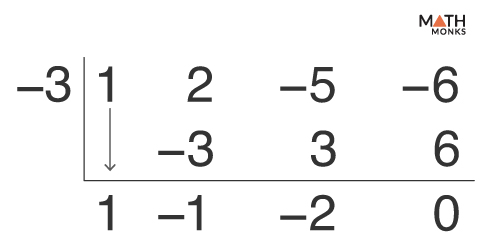
Given, h(x) = x3 + 2x2 – 5x – 6 and x = -3 is one of the roots …..(i)
By the factor theorem, h(x) = (x + 3)q(x); here, q(x) is a quadratic polynomial.
On dividing h(x) by (x + 3) by the synthetic division, we get
The quotient is x2 – x – 2, and the remainder is 0
Thus, x3 + 2x2 – 5x – 6
= (x + 3)(x2 – x – 2)
Now, using the quadratic formula,
x = ${\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$
⇒ x = ${\dfrac{-\left( -1\right) \pm \sqrt{\left( -1\right) ^{2}-4\times 1\times \left( -2\right) }}{2\times 1}}$
⇒ x = ${\dfrac{1\pm \sqrt{1+8}}{2}}$
⇒ x = ${\dfrac{1\pm \sqrt{9}}{2}}$
⇒ x = ${\dfrac{1\pm 3}{2}}$
⇒ x = 2 and -1 …..(ii)
Thus, x = -3, -1, and 2 are the roots of x3 + 2x2 – 5x – 6
![]() Find the value of k for which x = -2 is a root of the polynomial g(x) = 2x3 + kx2 – 3x + 4
Find the value of k for which x = -2 is a root of the polynomial g(x) = 2x3 + kx2 – 3x + 4
Solution:
![]()
Given g(x) = 2x3 + kx2 – 3x + 4 and x = -2 is one of the roots.
From the factor theorem, g(-2) = 0
Now, g(-2) = 2(-2)3 + k(-2)2 – 3(-2) + 4 = -16 + 4k + 6 + 4 = -6 + 4k
⇒ -6 + 4k = 0
⇒ 4k = 6
⇒ k = ${\dfrac{6}{4}}$
⇒ k = ${\dfrac{3}{2}}$Thus, the value of k is ${\dfrac{3}{2}}$