Derivative of a Polynomial

In calculus, the derivative of a polynomial represents the rate of change of the function with respect to its variable. 

For example, for the function f(x) = x², its derivative is f’(x) = 2x, indicating how the value of f(x) changes as x changes.

Here are the rules we follow to differentiate polynomials:

Power Rule

Statement

For any real number n, the derivative of f(x) = xⁿ is:

${f’\left( x\right) =\dfrac{d}{dx}\left( x^{n}\right) =n\cdot x^{n-1}}$

Proof 

For f(x) = xⁿ, where n is a positive integer, we have

${f’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{\left( x+h\right) ^{n}-x^{n}}{h}}$

Expanding (x + h)ⁿ using the binomial theorem,

${\left( x+h\right) ^{n}=x^{n}+nx^{n-1}h+\begin{pmatrix} n \\ 2 \end{pmatrix}x^{n-2}h^{2}+\begin{pmatrix} n \\ 3 \end{pmatrix}x^{n-3}h^{3}+\ldots +nxh^{n-1}+h^{n}}$

Subtracting xⁿ, 

⇒ ${\left( x+h\right) ^{n}-x^{n}=nx^{n-1}h+\begin{pmatrix} n \\ 2 \end{pmatrix}x^{n-2}h^{2}+\begin{pmatrix} n \\ 3 \end{pmatrix}x^{n-3}h^{3}+\ldots +nxh^{n-1}+h^{n}}$

Now, dividing both sides by h, 

${\dfrac{\left( x+h\right) ^{n}-x^{n}}{h}=\dfrac{nx^{n-1}h+\begin{pmatrix} n \\ 2 \end{pmatrix}x^{n-2}h^{2}+\begin{pmatrix} n \\ 3 \end{pmatrix}x^{n-3}h^{3}+\ldots +nxh^{n-1}+h^{n}}{h}}$

⇒ ${\dfrac{\left( x+h\right) ^{n}-x^{n}}{h}=nx^{n-1}+\begin{pmatrix} n \\ 2 \end{pmatrix}x^{n-2}h+\begin{pmatrix} n \\ 3 \end{pmatrix}x^{n-3}h^{2}+\ldots +nxh^{n-2}+h^{n-1}}$

Applying the limit definition of the derivative, we get

⇒ ${f’\left( x\right) =\lim _{h\rightarrow 0}\left( nx^{n-1}+\begin{pmatrix} n \\ 2 \end{pmatrix}x^{n-2}h+\begin{pmatrix} n \\ 3 \end{pmatrix}x^{n-3}h^{2}+\ldots +nxh^{n-2}+h^{n-1}\right)}$

⇒ f’(x) = nx^{n – 1} 

Thus, the power rule is derived.

Constant Rule

Statement

For any constant c, the derivative of f(x) = c is:

${f’\left( x\right) =\dfrac{d}{dx}\left( c\right) =0}$

Proof

For f(x) = c, where c is any constant, we have

f(x + h) = c

Now, applying the limit definition of the derivative, we get

${f’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h}}$

⇒ ${f’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{c-c}{h}}$

⇒ ${f’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{0}{h}}$

⇒ ${f’\left( x\right) =\lim _{h\rightarrow 0}0}$

⇒ ${f’\left( x\right) =0}$

Thus, the constant rule is derived.

Sum and Difference Rules

Statement

The derivative of the sum of functions is the sum of their derivatives:

${\dfrac{d}{dx}\left[ f\left( x\right) +g\left( x\right) \right] =\dfrac{d}{dx}f\left( x\right) +\dfrac{d}{dx}g\left( x\right)}$

⇒ ${\dfrac{d}{dx}\left[ f\left( x\right) +g\left( x\right) \right] =f’\left( x\right) +g’\left( x\right)}$

The derivative of the difference of functions is the difference of their derivatives:

${\dfrac{d}{dx}\left[ f\left( x\right) -g\left( x\right) \right] =\dfrac{d}{dx}f\left( x\right) -\dfrac{d}{dx}g\left( x\right)}$

⇒ ${\dfrac{d}{dx}\left[ f\left( x\right) -g\left( x\right) \right] =f’\left( x\right) -g’\left( x\right)}$

Proof 

Let us consider s(x) = f(x) ± g(x), where f(x) and g(x) are differentiable functions.

Applying the limit definition of the derivative, we get

${s’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{s\left( x+h\right) -s\left( x\right) }{h}}$

By substituting s(x + h) = f(x + h) ± g(x + h) and s(x) = f(x) ± g(x), we get

${s’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{\left[ f\left( x+h\right) \pm g\left( x+h\right) \right] -\left[ f\left( x\right) \pm g\left( x\right) \right] }{h}}$

Now, the derivative of the sum of functions is:

${s’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{\left[ f\left( x+h\right) +g\left( x+h\right) \right] -\left[ f\left( x\right) +g\left( x\right) \right] }{h}}$

Rearranging and regrouping the terms, 

⇒ ${s’\left( x\right) =\lim _{h\rightarrow 0}\left[ \dfrac{f\left( x+h\right) -f\left( x\right) }{h}+\dfrac{g\left( x+h\right) -g\left( x\right) }{h}\right]}$

Applying the sum law for limits and the definition of the derivative,

⇒ ${s’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h}+\lim _{h\rightarrow 0}\dfrac{g\left( x+h\right) -g\left( x\right) }{h}}$

⇒ ${s’\left( x\right) =f’\left( x\right) +g’\left( x\right)}$ …..(i)

Again, the derivative of the difference of functions is:

${s’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{\left[ f\left( x+h\right) -g\left( x+h\right) \right] -\left[ f\left( x\right) -g\left( x\right) \right] }{h}}$

Rearranging and regrouping the terms, 

⇒ ${s’\left( x\right) =\lim _{h\rightarrow 0}\left[ \dfrac{f\left( x+h\right) -f\left( x\right) }{h}-\dfrac{g\left( x+h\right) +g\left( x\right) }{h}\right]}$

Applying the difference law for limits and the definition of the derivative,

⇒ ${s’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h}-\lim _{h\rightarrow 0}\dfrac{g\left( x+h\right) -g\left( x\right) }{h}}$

⇒ ${s’\left( x\right) =f’\left( x\right) -g’\left( x\right)}$ …..(ii)

From (i) and (ii), we get

${\dfrac{d}{dx}\left[ f\left( x\right) \pm g\left( x\right) \right] =f’\left( x\right) \pm g’\left( x\right)}$

Thus, the sum and difference rule is derived.

Constant Multiple Rule

Statement

The derivative of a constant multiplied by a function is the constant multiplied by the derivative of the function:

${\dfrac{d}{dx}\left[ c\cdot f\left( x\right) \right] =c\cdot f’\left( x\right)}$

Proof

Let g(x) = c ⋅ f(x), where c is a constant and f(x) is differentiable. 

Applying the limit definition of the derivative, we get

${g’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{g\left( x+h\right) -g\left( x\right) }{h}}$

Now, substituting g(x) = c ⋅ f(x), we get

${g’\left( x\right) =\lim _{h\rightarrow 0}\dfrac{c\cdot f\left( x+h\right) -c\cdot f\left( x\right) }{h}}$

Since c is constant, factoring the constant out, we get

${g’\left( x\right) =c\cdot \lim _{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h}}$

Applying the limit definition of the derivative, we get

${g’\left( x\right) =c\cdot f’\left( x\right)}$

⇒ ${\dfrac{d}{dx}\left[ c\cdot f\left( x\right) \right] =c\cdot f’\left( x\right)}$

Thus, the constant multiple rule is derived.

Finding the Derivative of f(x) = 5x³ – 4x² + 7x – 2

f(x) = 5x³ – 4x² + 7x – 2

By the constant multiple rule,

f’(x) = 5(x³)’ – 4(x²)’ + 7(x)’ – (2)’

By the constant rule,

⇒ f’(x) = 5(x³)’ – 4(x²)’ + 7(x)’ – 0

By the power rule to each term, 

⇒ f’(x) = 5 ⋅ 3x^{3 – 1} – 4 ⋅ 2x^{2 – 1} + 7x^{1 – 1} 

Simplifying,

⇒ f’(x) = 15x² – 8x + 7

Thus, the derivative of f(x) = 5x³ – 4x² + 7x – 2 is

f’(x) = 15x² – 8x + 7

Again, let us consider another function g(x) = 2x⁴ – 3x³ + x – 5

By the constant multiple rule,

g’(x) = 2(x⁴)’ – 3(x³)’ + (x)’ – (5)’

By the constant rule,

⇒ g’(x) = 2(x⁴)’ – 3(x³)’ + (x)’ – 0

By the power rule to each term,

⇒ g’(x) = 2 ⋅ 4x^{4 – 1} – 3 ⋅ 3x^{3 – 1} + x^{1 – 1} 

Simplifying,

⇒ g’(x) = 8x³ – 9x² + 1

Thus, the derivative of g(x) = 2x⁴ – 3x³ + x – 5 is

g’(x) = 8x³ – 9x² + 1

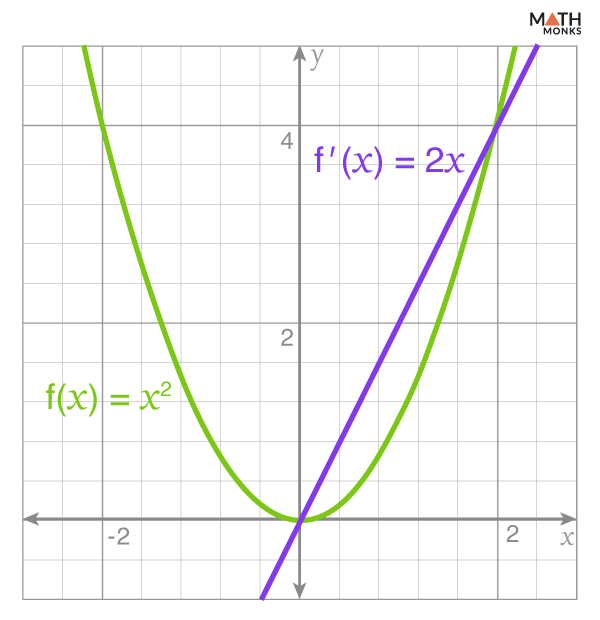
Graphical Representation

Geometrically, the derivative of a function represents the slope of the tangent line to the polynomial’s graph at any point. 

For example, if f(x) = x², its derivative is f’(x) = 2x 

When plotting f(x) and f’(x), we get

Here, the above graph indicates that the slope of the tangent line at any point x is 2x

Solved Examples