Legendre Polynomials

Legendre polynomials, denoted by P_n(x), are a family of orthogonal polynomials that are obtained as a solution to the Legendre differential equation (also called Legendre’s equation): 

${\left( 1-x^{2}\right) y”-2xy’+n\left( n+1\right) y=0}$

Or equivalently, 

${\dfrac{d}{dx}\left\{ \left( 1-x^{2}\right) \dfrac{dy}{dx}\right\} +n\left( n+1\right) y=0}$

Here, 

• n is a non-negative integer 
• The polynomials are defined on the closed interval [−1, 1] and exhibit orthogonality

Legendre polynomials are named after the French mathematician Adrien-Marie Legendre (1752–1833). These are widely used for expanding functions over the interval [-1, 1] due to their orthogonality and symmetric nature.

Similar to Legendre polynomials, each polynomial in this family, such as Chebyshev, Hermite, and Laguerre polynomials, solves second-order linear differential equations and is orthogonal under a specific weight function.

A few Legendre polynomials are listed here.

Properties

Orthogonality

Legendre polynomials belong to the class of orthogonal polynomials. They satisfy the orthogonality relation:

${\int _{-1}^{1}P_{m}\left( x\right) P_{n}\left( x\right) dx=\begin{cases}\dfrac{2}{n+1},if \  m=n\\ 0, \   \   \   \   \   \   \   \  if \  m\neq n\end{cases}}$

This property is used in approximation and solving boundary value problems.

Proof

As we know, Legendre polynomials P_n(x) are the solutions to the Legendre’s differential equation:

${\left( 1-x^{2}\right) \dfrac{d^{2}P_{n}}{dx^{2}}-2x\dfrac{dP_{n}}{dx}+n\left( n+1\right) P_{n}\left( x\right) =0}$, which is a self-adjoint.

Let us consider P_m(x) and P_n(x) as the solutions to the Legendre equation for different values of m and n 

${\left( 1-x^{2}\right) \dfrac{d^{2}P_{m}}{dx^{2}}-2x\dfrac{dP_{m}}{dx}+m\left( m+1\right) P_{m}\left( x\right) =0}$ …..(i)

${\left( 1-x^{2}\right) \dfrac{d^{2}P_{n}}{dx^{2}}-2x\dfrac{dP_{n}}{dx}+n\left( n+1\right) P_{n}\left( x\right) =0}$ …..(ii)

Multiplying equation (i) by P_n(x) and equation (ii) by P_m(x), we get

${P_{n}\left( x\right) \left[ \left( 1-x^{2}\right) \dfrac{d^{2}P_{m}}{dx^{2}}-2x\dfrac{dP_{m}}{dx}+m\left( m+1\right) P_{m}\left( x\right) \right] =0}$ …..(iii)

${P_{m}\left( x\right) \left[ \left( 1-x^{2}\right) \dfrac{d^{2}P_{n}}{dx^{2}}-2x\dfrac{dP_{n}}{dx}+n\left( n+1\right) P_{n}\left( x\right) \right] =0}$ …..(iv)

Now, subtracting equations (iii) and (iv), we get

${\left[ m\left( m+1\right) -n\left( n+1\right) \right] P_{m}\left( x\right) P_{n}\left( x\right) =\dfrac{d}{dx}\left( \left( 1-x^{2}\right) \left( P_{n}\left( x\right) \dfrac{dP_{m}}{dx}-P_{m}\left( x\right) \dfrac{dP_{n}}{dx}\right) \right)}$

Integrating both sides with respect to x from -1 to 1,

${\left( m\left( m+1\right) -n\left( n+1\right) \right) \int ^{1}_{-1}P_{m}\left( x\right) P_{n}\left( x\right) dx=\left[ \left( 1-x^{2}\right) \left( P_{n}\left( x\right) \dfrac{dP_{m}}{dx}-P_{m}\left( x\right) \dfrac{dP_{n}}{dx}\right) \right] _{-1}^{1}}$

Since the boundary terms vanish because P_m(x) and P_n(x) are finite at x = ± 1

Thus, ${\left( m\left( m+1\right) -n\left( n+1\right) \right) \int ^{1}_{-1}P_{m}\left( x\right) P_{n}\left( x\right) dx=0}$

Since m(m + 1) – n(n + 1) ≠ 0 for m ≠ n, it follows that

${\int ^{1}_{-1}P_{m}\left( x\right) P_{n}\left( x\right) dx=0}$, for m ≠ n …..(v)

When m = n, the integral ${\int ^{1}_{-1}\left( P_{n}\left( x\right) \right) ^{2}dx}$ gives the normalization factor. Using recursion, we get

${\int ^{1}_{-1}\left( P_{n}\left( x\right) \right) ^{2}dx=\dfrac{2}{2n+1}}$ …..(vi)

Thus, the equations (v) and (vi) complete the proof of the orthogonality of Legendre polynomials.

Rodrigues’ Formula

Legendre polynomials can be expressed using Rodrigues’ formula: 

${P_{n}\left( x\right) =\dfrac{1}{2^{n}n!}\dfrac{d^{n}}{dx^{n}}\left( \left( x^{2}-1\right) ^{n}\right)}$, n ∈ ℕ₀ 

By using this formula, it can be proved that P_n(x) is an n-degree polynomial. Here are a few Legendre polynomials listed. 

For n	${\dfrac{1}{2^{n}n!}}$	${\left( x^{2}-1\right) ^{n}}$	${\dfrac{d^{n}}{dx^{n}}\left( \left( x^{2}-1\right) ^{n}\right)}$	${P_{n}\left( x\right)}$
0	1	1	1	1
1	${\dfrac{1}{2}}$	(x2 – 1)	2x	x
2	${\dfrac{1}{8}}$	(x2 – 1)2 = x4 – 2x2 + 1	12x2 – 4	${\dfrac{1}{2}\left( 3x^{2}-1\right)}$
3	${\dfrac{1}{48}}$	(x2 – 1)3 = x6 – 3x4 + 3x2 – 1	120x3 – 72x	${\dfrac{1}{2}\left( 5x^{3}-3x\right)}$
4	${\dfrac{1}{384}}$	(x2 – 1)4 = x8 – 4x6 + 6x4 – 4x2 + 1	1680x4 – 1440x2 + 144	${\dfrac{1}{8}\left( 35x^{4}-30x^{2}+3\right)}$

Symmetry

Legendre polynomials satisfy symmetry properties: 

${P_{n}\left( -x\right) =\left( -1\right) ^{n}P_{n}\left( x\right)}$, which reflects their even or odd nature, depending on n.

For odd n, the polynomial is an odd function, whereas for even n, the polynomial is an even function.

Recurrence Relation

Legendre polynomials can be computed using the recurrence relation:

(2n + 1)xP_n(x) = (n + 1)P_{n + 1}(x) – nP_{n – 1}(x)

(2n – 1)xP_{n – 1}(x) = nP_n(x) + (n – 1)P_{n – 2}(x)

Here, n = 1, 2, …

Proof

To prove this, we can use Rodrigues’ formula. 

As we know, the leading coefficient of xⁿ in P_n(x) is ${\dfrac{1}{2^{n}n!}\dfrac{\left( 2n\right) !}{n!}}$

Thus, the leading coefficient of (x² – 1)ⁿ is x²ⁿ 

Now, ${\dfrac{dx^{2n}}{dx}}$ = 2nx^{2n – 1} 

${\dfrac{d^{2}x^{2n}}{dx^{2}}}$ = 2n(2n – 1)x^{2n – 1 – 1} = 2n(2n – 1)x^{2n – 2} 

The k^th derivative is ${\dfrac{d^{k}x^{2n}}{dx^{k}}=\left[ 2n\left( 2n-1\right) \ldots \left( 2n-k+1\right) \right] x^{2n-k}}$

Thus, the n^th derivative is given by

${\dfrac{d^{n}x^{2n}}{dx^{n}}=\left[ 2n\left( 2n-1\right) \ldots \left( n+1\right) \right] x^{n}}$

This proves that P_n(x) has degree n, and the leading coefficient of P_n(x) can be written as

${\dfrac{1}{2^{n}n!}\left[ 2n\left( 2n-1\right) \ldots \left( n+1\right) \right] =\dfrac{1}{2^{n}n!}\left[ 2n\left( 2n-1\right) \ldots \left( n+1\right) \right] \dfrac{n\left( n-1\right) \ldots 1}{n\left( n-1\right) \ldots 1}}$ = ${\dfrac{1}{2^{n}n!}\dfrac{\left( 2n\right) !}{n!}}$

In order to prove the three-term recursion formula, we consider the expression (2n – 1)xP_{n – 1}(x) – nP_n(x) 

The coefficient of the leading term for (2n – 1)xP_{n – 1}(x) is 

${\left( 2n-1\right) \dfrac{1}{2^{n-1}\left( n-1\right) !}\dfrac{\left( 2n-2\right) !}{\left( n-1\right) !}=\dfrac{1}{2^{n-1}\left( n-1\right) !}\dfrac{\left( 2n-1\right) !}{\left( n-1\right) !}=\dfrac{\left( 2n-1\right) !}{2^{n-1}\left[ \left( n-1\right) !\right] ^{2}}}$ …..(i)

The coefficient of the leading term for nP_n(x) is 

${\left( 2n\right) \dfrac{1}{2^{n}\left( n\right) !}\dfrac{\left( 2n\right) !}{\left( n\right) !}=n\left( \dfrac{2n}{2n^{2}}\right) \left( \dfrac{1}{2^{n-1}\left( n-1\right) !}\right) \dfrac{\left( 2n-1\right) !}{\left( n-1\right) !}\dfrac{\left( 2n-1\right) !}{2^{n-1}\left[ \left( n-1\right) !\right] ^{2}}}$ …..(ii)

From (i) and (ii), we get

While each term is a polynomial of degree n, the leading order terms in (2n – 1)xP_{n – 1}(x) – nP_n(x) vanish. 

The next terms will be of degree n – 2

Since P_n(x) is either even or odd functions, thus only containing even or odd powers of  x

(2n – 1)xP_{n – 1}(x) – nP_n(x) = polynomial of degree n – 2 …..(iii)

Since the Legendre polynomials form a basis, this polynomial in (iii) can be written as a linear combination of Legendre polynomials:

(2n – 1)xP_{n – 1}(x) – nP_n(x) = c₀P₀(x) + c₁P₁(x) + … + c_{n – 2}P_{n – 2}(x) …..(iv)

Multiplying equation (iv) by P_m(x) (here, m = 0, 1, 2, …, n – 3) and integrating with respect to x from -1 to 1, we get

0 = c_m||P_m(x)||², m = 0, 1, 2, …, n – 3 (using orthogonality)

Since all the c_m’s are 0, equation (iii) becomes

(2n – 1)xP_{n – 1}(x) – nP_n(x) = c_{n – 2}P_{n – 2}(x) …..(v)

By using the normalization condition, the final coefficient can be obtained as P_n(1) = 1

Thus, c_{n – 2} = (2n – 1) – n = n – 1

Now, from (v), we get

(2n – 1)xP_{n – 1}(x) – nP_n(x) = (n – 1)P_{n – 2}(x)

⇒ (2n – 1)xP_{n – 1}(x) = nP_n(x) + (n – 1)P_{n – 2}(x)

Generating Function

The generating function for Legendre polynomials is given by:

${\dfrac{1}{\sqrt{1-2xt+t^{2}}}=\sum ^{\infty }_{n=0}P_{n}\left( x\right) t^{n}}$

This function gives all Legendre polynomials P_n(x) in a single expression by expanding the left-hand side in powers of t.

For example,

Let us expand the left-hand side into a Taylor series around t = 0 and compute the coefficients of tⁿ, which correspond to P_n(x).

${\dfrac{1}{\sqrt{1-2xt+t^{2}}}\approx 1+xt+\dfrac{1}{2}\left( 3x^{2}-1\right) t^{2}+\ldots}$

Now, using the binomial theorem or direct substitution and comparing the coefficients of tⁿ, we get

P₀(x) = 1

P₁(x) = x

P₂(x) = ${\dfrac{1}{2}\left( 3x^{2}-1\right)}$

Series Solutions of Legendre Equation

By solving Legendre’s differential equation using a power series, the polynomials emerge as solutions that satisfy boundary conditions. 

Let us assume a power series solution ${P_{n}\left( x\right) =\sum ^{\infty }_{k=0}a_{k}x^{k}}$

Now, for n = 2,

P₂(x) = c₀(1 – 3x²)

Using normalization (where P_n(1) = 1), we get

P₂(x) = ${\dfrac{1}{2}\left( 3x^{2}-1\right)}$

The solution P₂(x) is thus obtained explicitly by using the power series solution.

Graphical Representation

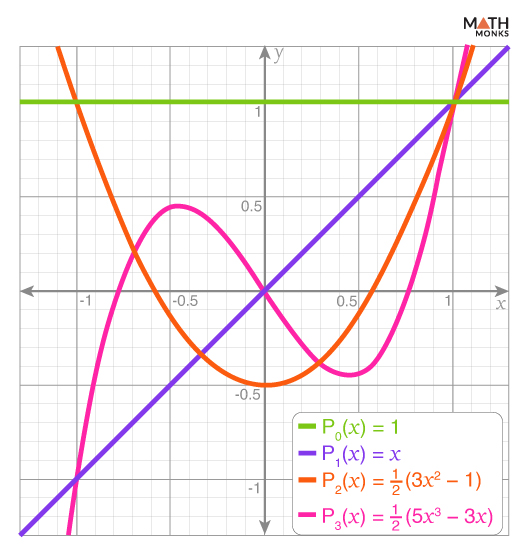
Graphs of the first few Legendre polynomials represent their properties visually, including orthogonality and symmetry. 

Following is a list of a few polynomials and their graphs:

n	Pn(x)	Nature of Graph
0	1	Constant
1	x	Linear
2	${\dfrac{1}{2}\left( 3x^{2}-1\right)}$	Parabolic
3	${\dfrac{1}{2}\left( 5x^{3}-3x\right)}$	Cubic

In the above graph,

• The area under the product of two distinct polynomials over [-1, 1] is zero, reflecting orthogonality.
• P_n(x) alternates between even and odd functions based on n.

Associated Legendre Functions

Associated Legendre polynomials are a class of functions that can be derived from the Legendre polynomials. It is written as

${P_{n}^{m}\left( x\right) =\left( 1-x^{2}\right) ^{\dfrac{m}{2}}\dfrac{d^{m}P_{n}\left( x\right) }{dx^{n}}}$

Here, 

m ≤ nP_n(x) is the Legendre polynomial of order n