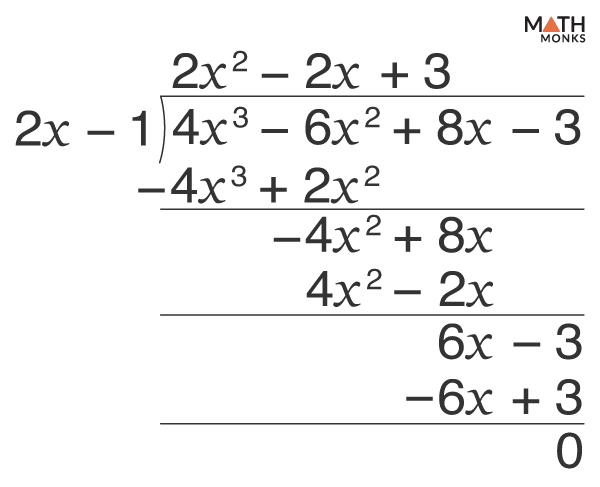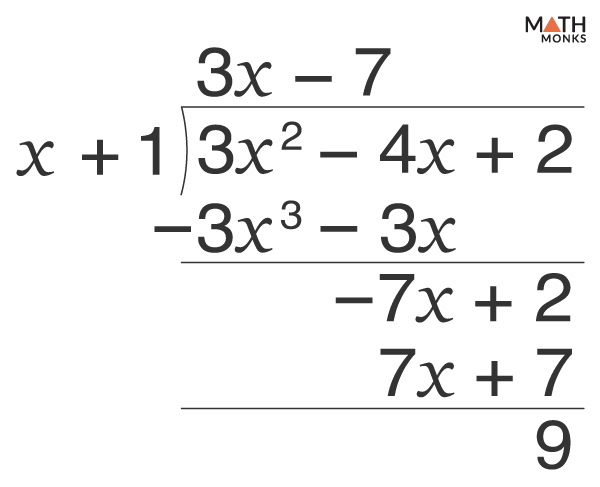Polynomials are expressions that consist of terms with variables raised to whole-number exponents.
The basic arithmetic operations with polynomials, addition, subtraction, multiplication, and division follow specific rules that help us effectively combine or separate polynomial expressions.
Adding
When adding polynomials, we combine the like terms (terms with the same variable raised to the same power).
There are two common methods for adding polynomials: the horizontal and the vertical methods.
Problem: Adding polynomials by the HORIZONTAL METHOD
![]()
Add: (2x2 – 3x + 1) and (x2 + 4x – 8)
Solution:
![]()
Given (2x2 – 3x + 1) and (x2 + 4x – 8) are the two polynomials
Writing the Polynomials Next to Each Other
(2x2 – 3x + 1) + (x2 + 4x – 8)
= 2x2 – 3x + 1 + x2 + 4x – 8
Combining the Like Terms
= (2x2 + x2) + (-3x + 4x) + (1 – 8)
= 3x2 + x – 7
Thus, the sum is 3x2 + x – 7
Problem: Adding polynomials by the VERTICAL METHOD
![]()
Add: (2x2 – 3x + 1) and (x2 + 4x – 8)
Solution:
![]()
Given (2x2 – 3x + 1) and (x2 + 4x – 8) are the two polynomials
Arranging the Like Terms Vertically
${\begin{aligned}2x^{2}-3x+1\\ \dfrac{+x^{2}+4x-8}{}\end{aligned}}$
Adding Each Column
${\begin{aligned}2x^{2}-3x+1\\ \dfrac{+x^{2}+4x-8}{3x^{2}+x-7}\end{aligned}}$
Thus, the sum is 3x2 + x – 7
Subtracting
To subtract polynomials, we distribute the subtraction sign across all terms in the second polynomial and then combine the like terms. Similar to addition, each term can be organized either by the horizontal or the vertical method.
Problem: Subtracting polynomials by the HORIZONTAL METHOD
![]()
Subtract (x2 – 3x + 4) from (2x2 + 4x – 8)
Solution:
![]()
Given that the polynomials are (x2 – 3x + 4) and (2x2 + 4x – 8)
Writing the Polynomials Next to Each Other
(2x2 + 4x – 8) – (x2 – 3x + 4)
Distributing the Subtraction Sign
= 2x2 + 4x – 8 – x2 + 3x – 4
Combining the Like Terms
= (2x2 – x2) + (4x + 3x) + (- 8 – 4)
= x2 + 7x – 12
Thus, the difference is x2 + 7x – 12
Problem: Subtracting polynomials by the VERTICAL METHOD
![]()
Subtract (x2 – 3x + 4) from (2x2 + 4x – 8)
Solution:
![]()
Given that the polynomials are (x2 – 3x + 4) and (2x2 + 4x – 8)
Arranging the Like Terms Vertically
${\begin{aligned}2x^{2}+4x-8\\ \dfrac{-\left( x^{2}-3x+4\right) }{}\end{aligned}}$
Changing the Signs
${\begin{aligned}2x^{2}+4x-8\\ \dfrac{-x^{2}+3x-4}{}\end{aligned}}$
Evaluating Each Column
${\begin{aligned}2x^{2}+4x-8\\ \dfrac{-x^{2}+3x-4}{x^{2}+7x-12}\end{aligned}}$
Thus, the difference is x2 + 7x – 12
Multiplying
Multiplying polynomials involves distributing each term in the first polynomial by each term in the second polynomial.
Problem: Multiplying MONOMIALS by MONOMIALS
![]()
Multiply 2x by 3xy
Solution:
![]()
Given, 2x ⋅ 3xy
Multiplying the Coefficients and Variables
= (2 ⋅ 3)(x ⋅ xy)
Keeping The Products
= (6) ⋅ (x2y)
= 6x2y
Problem: Multiplying MONOMIALS by BINOMIALS
![]()
Multiply: 3x(2xy + 5)
Solution:
![]()
Given, 3x(2xy + 5)
Multiplying Each Term by the Monomial
= 3x ⋅ 2xy + 3x ⋅ 5
Simplifying
= (3 ⋅ 2)(x ⋅ xy) + (3 ⋅ 5)x
= 6x2y + 15x
Thus, the product is 6x2y + 15x
Problem: Multiplying BINOMIALS by BINOMIALS by the FOIL METHOD
![]()
Multiply the polynomials (2x – 7) and (3x + 4)
Solution:
![]()
Given, (2x – 7)(3x + 4)
Multiplying Each Term of the Binomial by the Other
= 2x(3x + 4) – 7(3x + 4)
= 2x ⋅ 3x + 2x ⋅ 4 – 7 ⋅ 3x – 7 ⋅ 4
Simplifying
= (2 ⋅ 3)(x ⋅ x) + (2 ⋅ 4)x – (7 ⋅ 3)x – (7 ⋅ 4)
= 6x2 + 8x – 21x – 28
= 6x2 – 13x – 28
Thus, the product is 6x2 – 13x – 28
Problem: Multiplying POLYNOMIALS by MONOMIALS
![]()
Multiply: 2x2 + x – 4 by 3x3
Solution:
![]()
Given, 3x3(2x2 + x – 4)
Multiplying Each Term by the Monomial
= 3x3 ⋅ 2x2 + 3x3 ⋅ x – 3x3 ⋅ 4
Simplifying
= (3 ⋅ 2)(x3 ⋅ x2) + (3 ⋅ 1)(x3 ⋅ x) – (3 ⋅ 4)x3
= 6x5 + 3x4 – 12x3
Thus, the product is 6x5 + 3x4 – 12x3
Problem: Multiplying POLYNOMIALS by POLYNOMIALS
![]()
Multiply: x2 + 2x + 1 by x2 + 2x – 1
Solution:
![]()
Given, (x2 + 2x – 1)(x2 + 2x + 1)
Multiplying Each Term of the First Polynomial by the Other
= x2(x2 + 2x + 1) + 2x(x2 + 2x + 1) -1(x2 + 2x + 1)
= x2 ⋅ x2 + x2 ⋅ 2x + x2 ⋅ 1 + 2x ⋅ x2 + 2x ⋅ 2x + 2x ⋅ 1 – 1 ⋅ x2 – 1 ⋅ 2x – 1 ⋅ 1
Simplifying
= (x2 ⋅ x2) + 2(x2 ⋅ x) + 1x2 + 2(x ⋅ x2) + (2 ⋅ 2)(x ⋅ x) + (2 ⋅ 1)x – x2 – (1 ⋅ 2)x – 1
= x4 + 2x3 + x2 + 2x3 + 4x2 + 2x – x2 – 2x – 1
= x4 + (2x3 + 2x3) + (x2 + 4x2 – x2) + (2x – 2x) – 1
= x4 + 4x3 + 4x2 – 1
Thus, the product is x4 + 4x3 + 4x2 – 1
Dividing
Dividing polynomials can be done using long division or synthetic division.
Long division works for dividing any polynomial by another polynomial, while synthetic division is a shortcut that only applies when dividing by a binomial of the form x – c.
Problem: Dividing POLYNOMIALS using LONG DIVISION
![]()
Divide: 4x3 – 6x2 + 8x – 3 by 2x – 1
Solution:
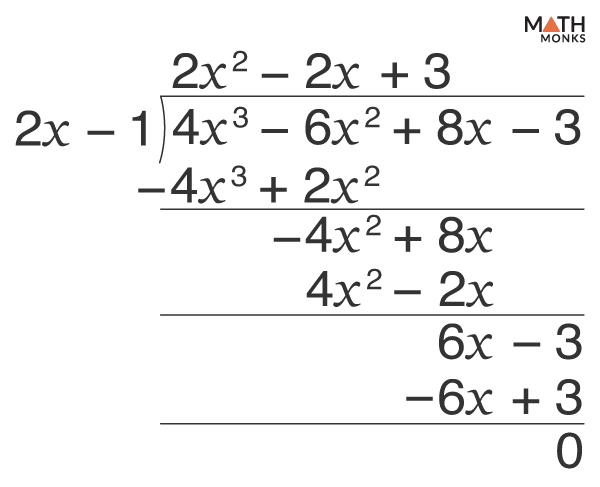
Here, the quotient is 2x2 – 2x + 3, and the remainder is 0
![]()
Divide:
3x2 – 4x + 2 by x + 1
Solution:
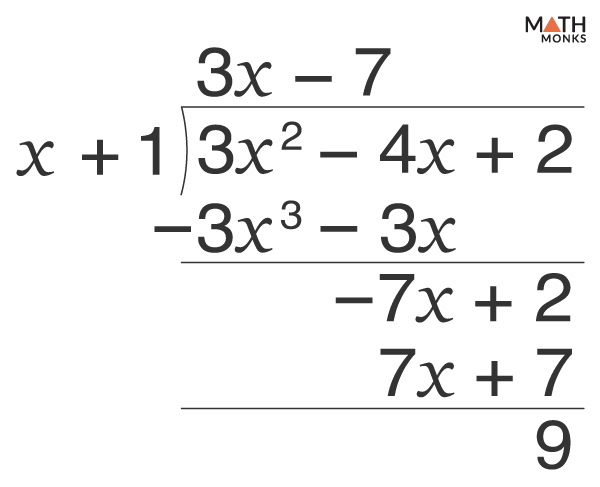
Here, the quotient is 3x – 7, and the remainder is 9
Problem: Dividing POLYNOMIALS using SYNTHETIC DIVISION
![]()
Divide: 3x2 + 4x – 6 by x – 2
Solution:
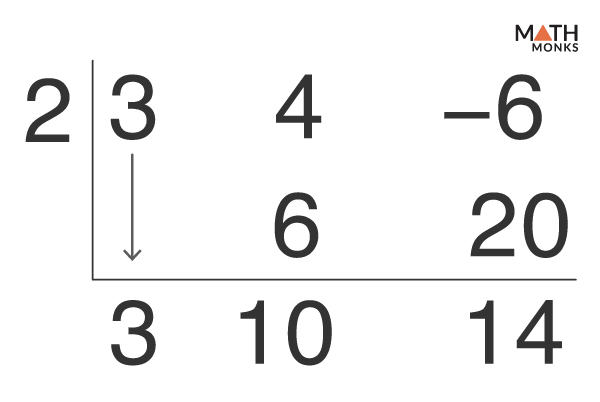
Here, the quotient is 3x + 10, and the remainder is 14
![]()
Which of these operations is not closed for polynomials?
a) Addition
b) Subtraction
c) Multiplication
d) Division
Solution:
![]()
As we know, adding, subtracting, and multiplying polynomials always result in polynomials, whereas dividing polynomials may or may not result in polynomials.
Thus, option d) is not closed for polynomials.
