Polynomial identities, or algebraic identities, are mathematical equations that hold true for all values of the variables involved. Unlike equations that are solved for specific values, identities are universally true, regardless of the specific numerical values of the variables.
These identities are used to simplify expressions and solve polynomial equations easily.
For example,
(a + b)2 = a2 + 2ab + b2 is a polynomial identity as it holds for all real or complex values of a and b
Here is a list of all the polynomial identities:
The above identities can be classified based on their degree or the highest power of the variable(s) involved.
For Second Degree
Second-degree polynomial identities are equations involving polynomials where the highest power of the variable is 2.
Here are the second-degree polynomial identities:
Square of a Binomial
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
Difference of Squares
Square of a Trinomial
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
- (a – b – c)2 = a2 – b2 – c2 – 2ab + 2bc – 2ca
Product of Binomials
- (x + a)(x + b) = x2 + (a + b)x + ab
For Third Degree
Third-degree polynomial identities are equations involving polynomials where the highest power of the variable is 3.
Here are the third-degree polynomial identities:
Cube of a Binomial
- (a + b)3 = a2 + 3a2b + 3ab2 + b3
- (a – b)3 = a2 – 3a2b + 3ab2 – b3
Sum and Difference of Cubes
- a3 + b3 = (a + b)(a2 – ab + b2)
- a3 – b3 = (a – b)(a2 + ab + b2)
Other Form
- a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
For n Degree
Thus, like first and second-degree polynomials, n-degree polynomial identities are those in which the maximum power of a variable in a term is ‘n,’ where n is any natural number.
Here are the n-degree polynomial identities:
Difference of Powers
an – bn = (a – b)(an – 1 + an – 2b + … + abn – 2 + bn – 1)
Powers of Binomial
${\left( a+b\right) ^{n}=\sum ^{n}_{k=0}\begin{pmatrix} n \\ k \end{pmatrix}a^{n-k}b^{k}}$, derived from the binomial theorem.
Here,
- n ∈ ℕ
- If n is even, then n = 2k
- If n is odd, then n = 2k + 1
Proofs
Let us now prove some common polynomial identities discussed above.
Square of a Binomial
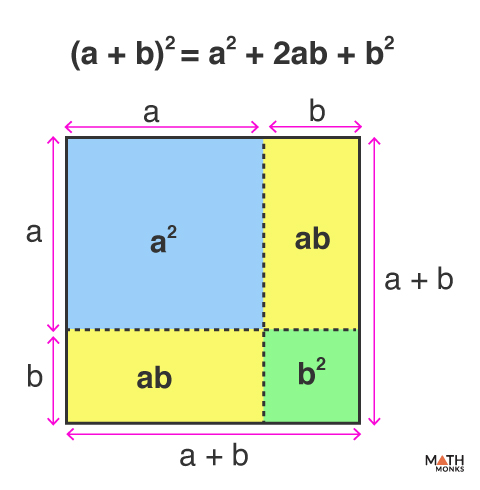
(a + b)2 = a2 + 2ab + b2
Writing the L.H.S in factor form,
(a + b)2
= (a + b)(a + b)
Using the distributive property,
= a(a + b) + b(a + b)
= a2 + ab + ba + b2
Since ab = ba, combining like terms,
= a2 + 2ab + b2
Thus, (a + b)2 = a2 + 2ab + b2
This can be visualized using a square with sides measuring (a + b) units and thus an area of (a + b)2 sq. units.
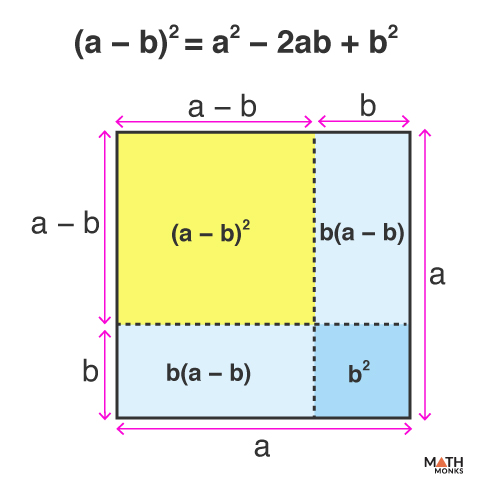
(a – b)2 = a2 – 2ab + b2
Expanding the expression on L.H.S.,
(a – b)2
= (a – b)(a – b)
Using the distributive property,
= a(a – b) – b(a – b)
= a2 – ab – ba + b2
Since ab = ba, combining like terms,
= a2 – 2ab + b2
Thus, (a – b)2 = a2 – 2ab + b2
This can be visualized using a square with sides measuring (a – b) units and thus an area of (a – b)2 sq. units.
Difference of Squares
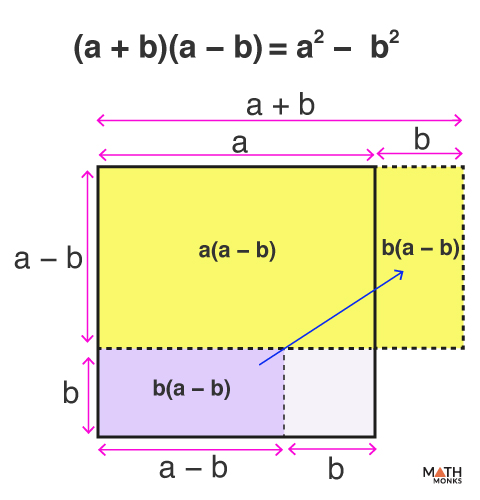
(a + b)(a – b) = a2 – b2
Factoring the L.H.S.,
(a + b)(a – b)
Using the distributive property,
= a(a – b) + b(a – b)
= a2 – ab + ba – b2
Since ab = ba, combining like terms,
= a2 – b2
Thus, (a + b)(a – b) = a2 – b2
This can be visualized using a rectangle of sides (a + b) units and (a – b) units and area (a + b)(a – b) sq. units.
Thus, by rearranging the individual squares and rectangles, we get
(a + b)(a – b) = a2 – b2
Product of Binomials
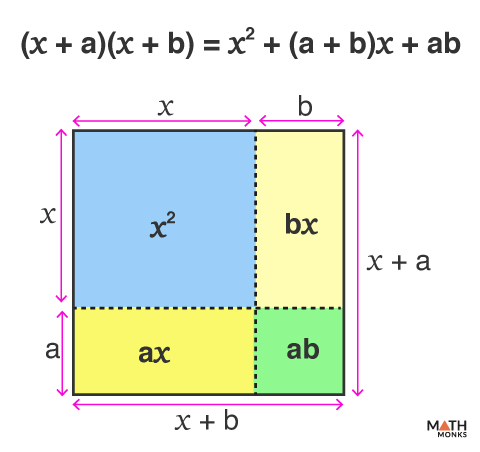
(x + a)(x + b) = x2 + (a + b)x + ab
Expanding the expression on the L.H.S.,
(x + a)(x + b)
Using the distributive property,
= x(x + b) + a(x + b)
= x2 + bx + ax + ab
Combining like terms,
= x2 + x(b + a) + ab
= x2 + (a + b)x + ab
Thus, (x + a)(x + b) = x2 + (a + b)x + ab
This can be visualized with a rectangle of sides (x + a) units and (x + b) units. Thus, the area of the rectangle is (x + a)(x + b) = x2 + (a + b)x + ab sq. units.
Applications
Polynomial identities are commonly used to simplify or rewrite complex polynomial expressions efficiently.
For Expanding Polynomials
Let us expand (x + 4)2
As we know, (a + b)2 = a2 + 2ab + b2
Now, if we consider a = x and b = 4, then
(x + 4)2
= x2 + (2)(x)(4) + 42
= x2 + 8x + 16
Again, let us now expand the expression (p + 2)(p + 5)
As we know, (x + a)(x + b) = x2 + (a + b)x + ab
Now, if we consider x = p, a = 2, and b = 5, then
(p + 2)(p + 5)
= p2 + (2 + 5)p + (2)(5)
= p2 + 7p + 10
For Factoring Polynomials
Let us factor the expression x4 – y4
As we know, a2 – b2 = (a + b)(a – b)
Now, considering a = x2 and b = y2, we get
x4 – y4
= (x2)2 – (y2)2
= (x2 + y2)(x2 – y2)
= (x2 + y2)(x + y)(x – y)
Thus, x4 – y4 can be factored as (x2 + y2)(x + y)(x – y)
Now, let us expand x3 – 27
As we know, a3 – b3 = (a – b)(a2 + ab + b2)
x3 – 27
= (x)3 – (3)3
Now, considering a = x and b = 3, we get
= (x – 3)(x2 + 3x + 9)
Solved Examples
![]()
Show that (a2 + b2)2 = (a2 – b2)2 + (2ab)2 is a polynomial identity.
Solution:
![]()
Here, from L.H.S.,
(a2 + b2)2
= (a2 + b2)(a2 + b2)
Expanding by the distributive property,
= a2(a2 + b2) + b2(a2 + b2)
= a4 + a2b2 + b2a2 + b4
Combining like terms,
= a4 + 2a2b2 + b4 …..(i)
Now, from R.H.S.,
(a2 – b2)2 + (2ab)2
= (a2 – b2)(a2 – b2) + (2ab)2
Expanding by the distributive property,
= a2(a2 – b2) – b2(a2 – b2) + (2ab)2
= a4 – a2b2 – b2a2 + b4 + 4a2b2
= a4 + (-a2b2 – b2a2 + 4a2b2) + b4
Combining like terms,
= a4 + 2a2b2 + b4 …..(ii)
Thus, from (i) and (ii), we get
(a2 + b2)2 = (a2 – b2)2 + (2ab)2 is a polynomial identity.
![]()
Determine whether (2x2 + y3)(2x2 – y3) = 4x2 – y3 is an identity.
Solution:
![]()
Here, from L.H.S.,
(2x2 + y3)(2x2 – y3)
Expanding by the distributive property,
= 2x2(2x2 – y3) + y3(2x2 – y3)
= 4x4 – 2x2y3 + 2x2y3 – y6
Combining like terms,
= 4x4 + (-2x2y3 + 2x2y3) – y6
= 4x4 – y6 ≠ R.H.S.
Thus, (2x2 + y3)(2x2 – y3) = 4x2 – y3 is not an identity.
![]()
Check whether (x + y)4 + (x – y)4 = 2x4 + 12x2y2 + 2y4 is an identity.
Solution:
![]()
Here, from L.H.S.,
(x + y)4 + (x – y)4
= [(x + y)2]2 + [(x – y)2]2
= (x2 + 2xy + y2)2 + (x2 – 2xy + y2)2 [using the identity of (a + b)2 and (a – b)2]
= (x2 + 2xy + y2)(x2 + 2xy + y2) + (x2 – 2xy + y2)(x2 – 2xy + y2)
Using the distributive property,
= x2(x2 + 2xy + y2) + 2xy(x2 + 2xy + y2) + y2(x2 + 2xy + y2) + x2(x2 – 2xy + y2) – 2xy(x2 – 2xy + y2) + y2(x2 – 2xy + y2)
= x4 + 2x3y + x2y2 + 2x3y + 4x2y2 + 2xy3 + y2x2 + 2xy3 + y4 +x4 – 2x3y + x2y2 – 2x3y + 4x2y2 – 2xy3 + y2x2 – 2xy3 + y4
Combining like terms,
= (x4 + x4) + (2x3y + 2x3y – 2x3y – 2x3y) + (x2y2 + 4x2y2 + y2x2 + x2y2 + 4x2y2 + y2x2) + (2xy3 + 2xy3 – 2xy3 – 2xy3) + (y4 + y4)
= 2x4 + 12x2y2 + 2y4
= R.H.S.
Thus, (x + y)4 + (x – y)4 = 2x4 + 12x2y2 + 2y4 is an identity.
![]()
Use polynomial identities to factor the following polynomials:
a) 27x9 – 343y6
b) 64 + 27a3
Solution:
![]()
a) Given, 27x9 – 343y6
= (3x3)3 – (7y2)3
Using the identity a3 – b3 = (a – b)(a2 + ab + b2), we get
= (3x3 – 7y2)[(3x3)2 + (3x3)(7y2) + (7y2)3]
= (3x3 – 7y2)(9x6 + 21x3y2 + 49y6)
Thus, 27x9 – 343y6 = (3x3 – 7y2)(9x6 + 21x3y2 + 49y6)
b) Given, 64 + 27a3
= (4)3 + (3a)3
Using the identity a3 + b3 = (a + b)(a2 – ab + b2), we get
= (4 + 3a)[(4)2 – (4)(3a) + (3a)2]
= (4 + 3a)(16 – 12a + 9a2)
Thus, 64 + 27a3 = (4 + 3a)(16 – 12a + 9a2)
![]()
Use polynomial identities to expand the polynomial (1 + p)4
Solution:
![]()
Given, (1 + p)4
= [(1 + p)2]2
Using the identity (a + b)2 = a2 + 2ab + b2, we get
= [1 + 2p + p2]2
Using the identity (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca, we get
= 1 + (2p)2 + (p2)2 + 2(1)(2p) + 2(2p)(p2) + 2(p2)(1)
= 1 + 4p2 + p4 + 4p + 4p3 + 2p2
= p4 + 4p3 + (4p2 + 2p2) + 1
= p4 + 4p3 + 6p2 + 1
![]()
Which of the following is not a polynomial identity?
a) (x + y)2 = x2 + 2xy + y2
b) (x – y)3 = x3 – 3x2y + 3xy2 – y3
c) x2 – y2 = (x + y)2(x – y)
Solution:
![]()
As we know, x2 – y2 = (x + y)(x – y)
Thus, option c) is not a polynomial identity.
