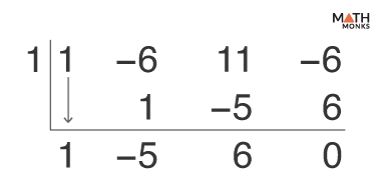Solving Polynomials

Solving polynomial equations involves finding the values of the variable(s) that satisfy the given equation. These values are known as the roots or solutions. 

The methods for solving polynomial equations depend on the degree of the polynomial, which is the highest power of the variable in the expression.

Linear Polynomials (Degree 1)

Let us solve the linear polynomial (degree 1) 2x + 3 = 0  

Isolating the Variable x 

Subtracting 3 from both sides, we get

2x + 3 – 3 = 0 – 3

⇒ 2x = -3

Solving for the Variable x 

On dividing both sides by 2, we get

⇒ ${\dfrac{2x}{2}=-\dfrac{3}{2}}$

⇒ ${x=-\dfrac{3}{2}}$

Thus, the solution is ${x=-\dfrac{3}{2}}$

However, solving higher-degree polynomials is a little more complex.

Quadratic Polynomials (Degree 2)

By Factoring

Factoring involves rewriting the polynomial as a product of binomials and applying the Zero Product Property, which states that if the product of two factors equals zero, then at least one of the factors must be zero. 

If a ⋅ b = 0, then either a = 0 or b = 0 (or both)

Now, let us solve the quadratic polynomials x² + 6x + 8 = 0

Splitting the Middle-Term 

⇒ x² + 4x + 2x + 8 = 0

Factoring the Polynomial 

⇒ x(x + 4) + 2(x + 4) = 0

⇒ (x + 4)(x + 2) = 0

Using Zero Product Property

⇒ (x + 4) = 0 or (x + 2) = 0

Solving for the Variable x 

⇒ x = -4 or x = -2

Thus, the solutions are x = -4, x = -2

By Quadratic Formula

The quadratic formula is another method for solving quadratic polynomial equations of the form:

ax² + bx + c = 0

Here, the roots can be found by 

${x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$

Let us solve 2x² – 4x – 6 = 0

Comparing With the Standard Form

Here, a = 2, b = -4, and c = -6

Substituting in the Formula 

${x=\dfrac{-\left( -4\right) \pm \sqrt{\left( -4\right) ^{2}-4\times 2\times \left( -6\right) }}{2\times 2}}$

Simplifying 

⇒ ${x=\dfrac{4\pm \sqrt{16+48}}{4}}$

⇒ ${x=\dfrac{4\pm \sqrt{64}}{4}}$

⇒ ${x=\dfrac{4\pm 8}{4}}$

⇒ x = 3 or x = -1

Thus, the solutions are x = 3, x = -1

For Higher-Degree Polynomials (Degree > 2)

By Grouping Terms

This method involves factoring by grouping and applying the Zero Product Property.

Let us solve the cubic polynomial x³ + 2x² – x – 2 = 0

Grouping Terms

⇒ (x³ + 2x²) – (x + 2) = 0

Factoring Each Group

⇒ x²(x + 2) – 1(x + 2) = 0

⇒ (x + 2)(x² – 1) = 0

⇒ (x + 2)(x + 1)(x – 1) = 0

Using Zero Product Property

⇒ (x + 2) = 0, (x + 1) = 0, or (x – 1) = 0

Solving for the Variable x 

⇒ x = -2, x = -1, or x = 1

Thus, the solutions are x = -2, x = -1, or x = 1

By Synthetic Division

This method helps us solve higher-degree polynomials when one root is known. Here, we divide a polynomial by a linear factor of the form (x – r), where r is the known root. 

Let us solve x³ – 6x² + 11x – 6 = 0 when x = 1 is one of the roots.

Perform Synthetic Division

Here,

• The coefficients of the polynomial are 1, -6, 11, and -6
• The suspected root is x = 1

Factoring the Polynomial

Now, x³ – 6x² + 11x – 6 = 0

⇒ (x – 1)(x² – 5x + 6) = 0

Factoring Each Group

⇒ (x – 1)(x² – 3x – 2x + 6) = 0

⇒ (x – 1) [x(x – 3) – 2(x – 3)] = 0

⇒ (x – 1)(x – 3)(x – 2) = 0

Using Zero Product Property

⇒ (x – 1) = 0, (x – 3) = 0, or (x – 2) = 0

⇒ x = 1, x = 3, or x = 2

Thus, the solutions are x = 1, x = 3, or x = 2

Solved Examples