A factor tree, also called a number tree, is a diagrammatic representation of all the factors of a number. The factors, when multiplied, give back the original number.
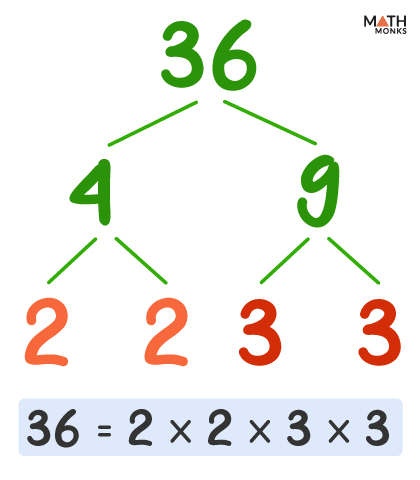
It is particularly used to show the prime factorization of a number. Shown below is a factor tree showing the prime factorization of 36
Here, 2, 2, 3, and 3 are the prime factors of 36.
A factor is also used for simplifying fractions and finding the least common multiple (LCM) and greatest common factor (GCF).
Note: We can also prime factor a number using the division method.
Steps To Do
Here are the steps we follow to create a factor tree.
Step 1: Choosing the Number
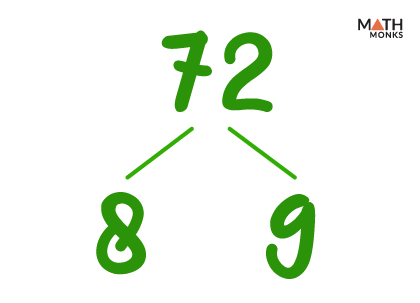
Let us factor the number 72 using the factor tree
Step 2: Placing the Number on the Top of the Tree
We begin by placing 72 at the top of the tree, followed by two downward branches to write its two factors.
Step 3: Finding Two Factors
Next, we will think of two numbers that, when multiplied together, will give back the original number.
For 72, we can use 8 × 9, as 8 × 9 = 72
Thus, 8 and 9 are the first two factors, which we will write below the branches.
Step 4. Splitting Each Composite Factor into Smaller Factors
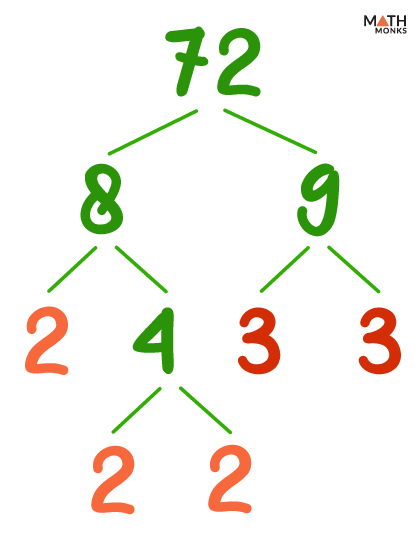
Then, we will look at each factor and decide if it can be further divided into 2 more factors.
Here,
8 is further split into 2 × 4, as 2 × 4 = 8 and
9 is further split into 3 × 3, as 3 × 3 = 9
Step 5. Continue Splitting Until All Numbers Are Prime
We further break each composite factor down into two factors.
Thus, 4 is split into 2 × 2, which are prime factors (as they cannot be divided any further)
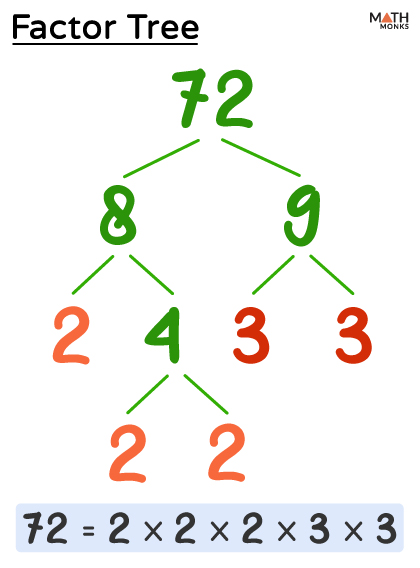
Thus, 72 can be expressed as the product of its prime factors:
72 = 2 × 2 × 2 × 3 × 3
Here, the factor tree of 72 will look like this:
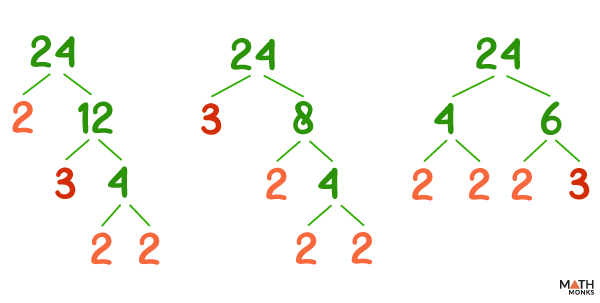
Note: A number can be represented using different factor trees, but they will always result in the same prime factors. This means the structure of the factor tree may vary depending on the factors chosen at each step of the breakdown.
Here are three different factor trees of 24:
Solved Examples
![]() Draw a factor tree of each number:
Draw a factor tree of each number:
a) 45
b) 90
c) 120
d) 108
Solution:
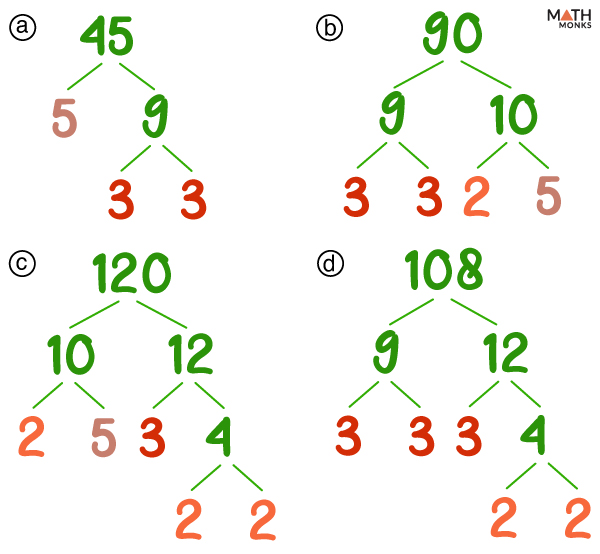
Thus, the prime factors are:
a) 45 = 3 × 3 × 5
b) 90 = 2 × 3 × 3 × 5
c) 120 = 2 × 2 × 2 × 3 × 5
d) 108 = 2 × 2 × 3 × 3 × 3
![]() Find the prime factorization of 75 using the factor tree.
Find the prime factorization of 75 using the factor tree.
Solution:
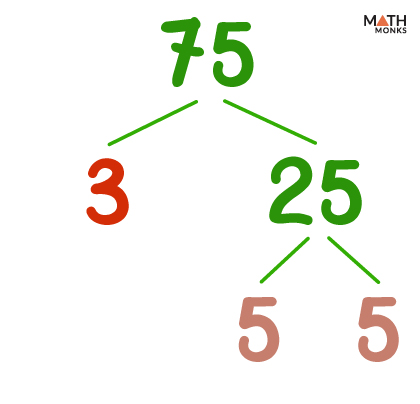
Thus, the prime factorization of 75 is:
75 = 3 × 5 × 5