The complement of a set is the set consisting of all elements present in the universal set but not in the original set.
Symbol
When writing the complement of a set, an apostrophe (‘) or a superscript c (c) notation is used.
If ‘A’ is a set, then its complement is represented by the symbol A’ or Ac and is mathematically expressed as
A’ = {x | x ∈ U and x ∉ A}
Here,
- U is the universal set, and
- x represents the elements in the universal set U but not in set A
Thus, the complement of set A is the difference between the universal set and set A. It is written as A’ = U – A.
It has many applications in set theory and topological spaces.
Example
For example, if A = {a, e, i, o, u} and the universal set is U = {a, c, d, e, i, n, o, t, u}, then A’ = {c, d, n, t}
Thus, to find the complement of a given set, we need to identify the elements in the universal set that are absent in the original set.
Complement of a Set Venn Diagram
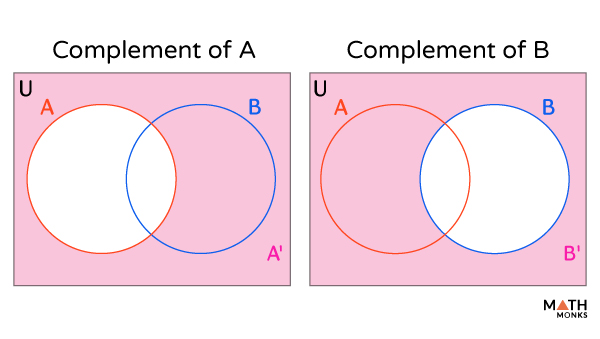
In a Venn diagram, a rectangular box represents the universal set, and its subsets are denoted by a circle. The complement of a set is the area of the universal set outside set A.
If ‘A’ is a set, the complement of set A is shown.
If two sets intersect (have some elements common), their complements are represented as:
Cardinality
If ‘A’ is a set and ‘U’ is the universal set, the cardinality of sets A and U are n(A) and n(U)
Thus, the cardinality of the complement of set A is denoted by n(A’) and is written as
n(A’) = n(U) – n(A)
Or, |A’| = |U| – |A|
For example,
If A = {a, e, i, o, u} and U = {a, c, d, e, i, n, o, t, u}, then the cardinality of A’ is
n(A’) = n(U) – n(A) = 9 – 5 = 4
Properties
Complement Laws
Union: The union of a set A and its complement A’ equals the universal set.
A ∪ A’ = U
Intersection: The intersection of a set A and its complement A’ is an empty set.
A ∩ A’ = ɸ
Double Complementation Law
The complement of the complement of set A gives back the original set.
(A’)’ = A
Law of Empty Set and Universal Set
The complement of the universal set produces an empty set or null set. Similarly, the complement of an empty set is the universal set.
U’ = ɸ and ɸ’ = U
De Morgan’s Law
For Union of Sets
The complement of the union of two sets is the intersection of their complements. If ‘A’ and ‘B’ are two sets, then
(A ∪ B)’ = A’ ∩ B’
For Intersection of Sets
The complement of the intersection of two sets is the union of their complements. If ‘A’ and ‘B’ are two sets, then
(A ∩ B)’ = A’ ∪ B’
Solved Examples
![]() Find the complement of set A when A = {1, 5, 9, 13} and U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
Find the complement of set A when A = {1, 5, 9, 13} and U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
Solution:
![]()
Here, A = {1, 5, 9, 13} and U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
Now, the complement of A is
A’ = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13} – {1, 5, 9, 13}
= {2, 3, 4, 6, 7, 8, 10, 11, 12}
Thus, the complement of set A is A’ = {2, 3, 4, 6, 7, 8, 10, 11, 12}
![]() If the universal set U = {students who attended the annual sports day in school} and a set A = {students who played cricket}, use the Venn diagram to represent the set of all students who attend all the sports in school except cricket.
If the universal set U = {students who attended the annual sports day in school} and a set A = {students who played cricket}, use the Venn diagram to represent the set of all students who attend all the sports in school except cricket.
Solution:
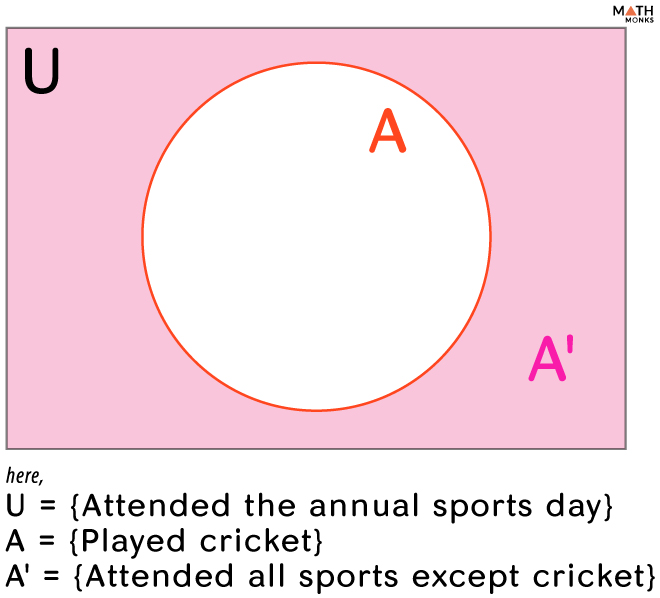
Given U = {students who attended the annual sports day in school} and A = {students who played cricket}
Here, the set of all students who attend all the sports in school except cricket is
A’ = U – A
= {students who attended the annual sports day in school} – {students who played cricket}