The cartesian product of two or more sets is a set of all ordered pairs in which the first element comes from the first set and the next from the second.
Symbol
If A and B are two sets, their cartesian product is written as A × B. It is also called the cross-product.
Formula
In the set builder notation, A × B is written as:
A × B = {(a,b) | a ∈ A, b ∈ B}
Here, a belongs to set A, and b belongs to set B.
For Two Sets
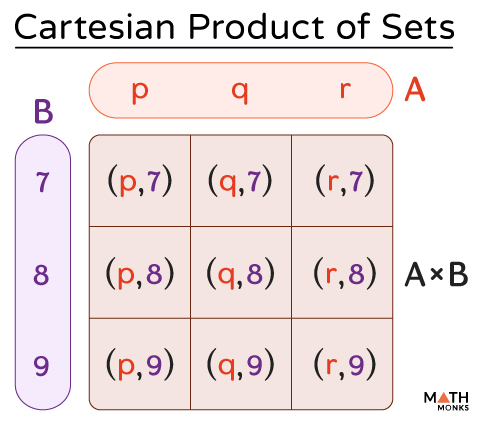
If A = {p, q, r} and B = {7, 8, 9} are two non-empty sets, then their cartesian product is:
A × B = {(p, 7), (p, 8), (p, 9), (q, 7), (q, 8), (q, 9)}
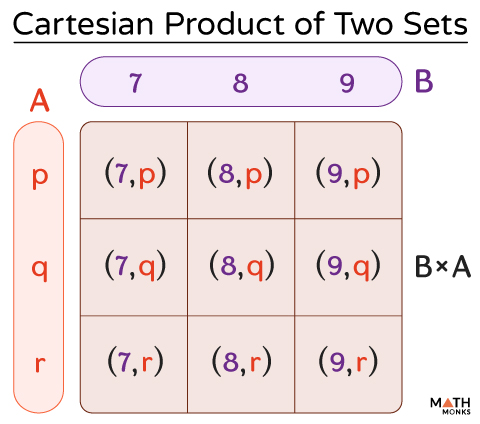
Similarly, we can find the cartesian product of B × A.
B × A = {(7, p), (7, q), (7, r), (8, p), (8, q), (8, r), (9, p), (9, q), (9, r)}
Thus, in general, A × B ≠ B × A
Set With Itself
If both sets are the same, A = B, then A × B is called the cartesian square of set A, and it is written as A2
A2 = A × A = {(a,b): a ∈ A, b ∈ A}
Here, we also conclude that if A = B, then A × B = B × A
Empty Set
The cartesian product of any set and an empty set produces the empty set. If A is a set and ɸ is an empty set, then A × ɸ = {(a, b) | a ∈ A, b ∈ ɸ}
In general, the cartesian product of two sets results in an empty set if and only if either of the sets is null.
Symbolically, if A = ɸ or B = ɸ, then A × B = ɸ
For Three Sets
The cartesian product can be defined and extended to more than two sets. The cartesian product of more than two sets is a larger set containing every ordered pair of all the given set elements.
In the set builder notation, A × B × C is written as:
A × B × C = {(a,b,c) | a ∈ A, b ∈ B, c ∈ C}
Example
If A = {5, 6}, B = {s, t}, and C = {g, h}, to find the cartesian product of A × B × C, we first find the cartesian product of A × B followed by the (A × B) × C
A × B = {(5, s), (5, t), (6, s), (6, t)}
Now, A × B × C = {(5, s), (5, t), (6, s), (6, t)} × {g, h}
⇒ A × B × C = {(5, s, g), (5, s, h), (5, t, g), (5, t, h), (6, s, g), (6, s, h), (6, t, g), (6, t, h)}
Properties
Commutative
The cartesian product depends on the order of sets, and it is thus non-commutative.
If A and B are two sets, then A × B ≠ B × A
Associative
The cartesian product is not associative. If A, B, and C are three sets, then (A × B) × C ≠ A × (B × C)
Distributive
Intersection of Sets
If A, B, and C are three sets, then according to the distributive property of the intersection of sets A × (B ∩ C) = (A × B) ∩ (A × C)
Union of Sets
If A, B, and C are three sets, then according to the distributive property of the union of sets A × (B ∪ C) = (A × B) ∪ (A × C)
Cardinality
The cardinality of the cartesian product of sets A and B is the total number of ordered pairs in A × B.
If x is the number of elements in set A, and y is the number of elements in set B, then the cardinality of the Cartesian product of sets A and B is xy.
Mathematically, it is written as if n(A) = x, n(B) = y, then n(A × B) = n(A) × n(B) = xy.
Similarly, for n number of sets, n(A1×…× An) = n(A1) × … × n(An)
Solved Examples
![]() Find the cartesian product of sets A and B. Given A = {1, 3, 7} and B = {4, 8}.
Find the cartesian product of sets A and B. Given A = {1, 3, 7} and B = {4, 8}.
Solution:
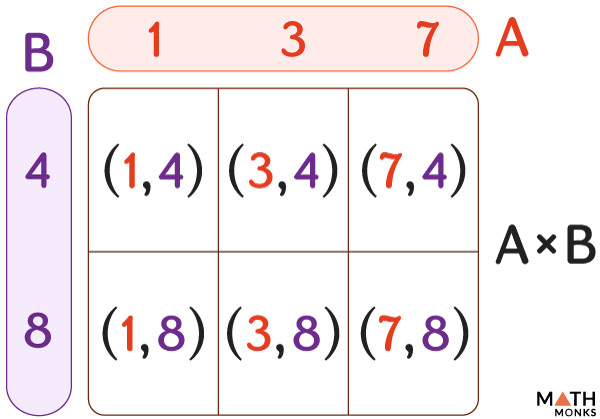
Thus, A × B = {(1, 4), (1, 8), (3, 4), (3, 8), (7, 4), (7, 8)}
![]() Find D2 when D = {c, g, k}.
Find D2 when D = {c, g, k}.
Solution:
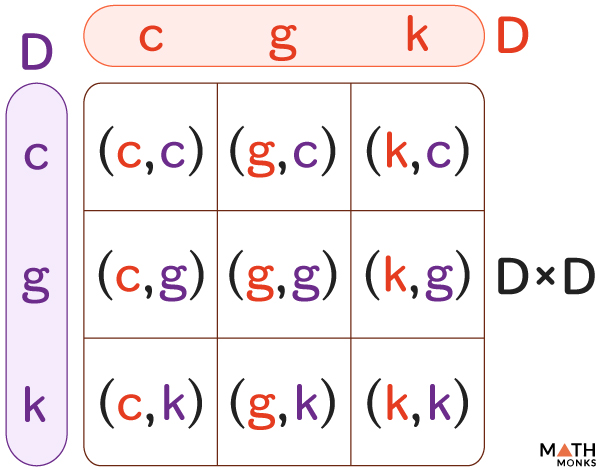
Thus, D2 = {(c, c), (c, g), (c, k), (g, c), (g, g), (g, k), (k, c), (k, g), (k, k)}