Set Difference

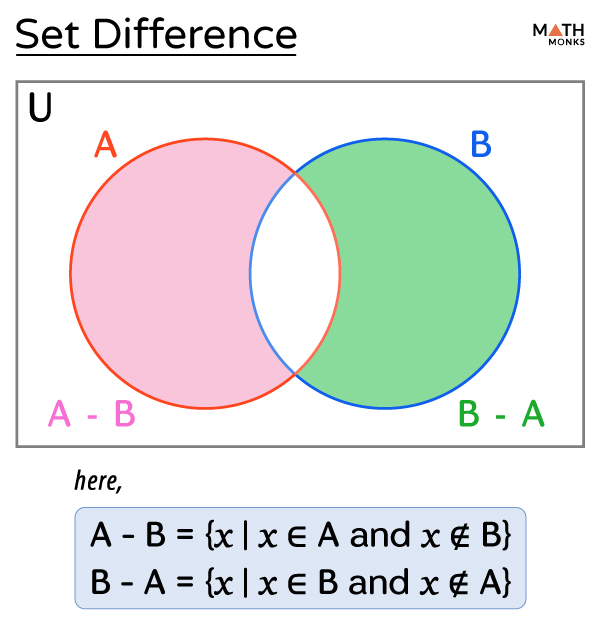
The difference between the two sets, ‘A’ and ‘B,’ represented by A – B or A ∖ B, is a set containing elements that are present in set A but absent in set B. To find the difference, we remove all elements of set B from set A, and the resulting set consists of the elements that belong only to A.

Mathematically, the set A – B or A ∖ B read as ‘A minus B’ is represented in set-builder form as:

A – B = {x | x ∈ A and x ∉ B}

Similarly, B – A =  {x | x ∈ B and x ∉ A}

Here are the representations of A – B and B – A with a Venn diagram.

Order

Like subtracting numbers, finding the difference between two or more sets requires maintaining the correct order. 

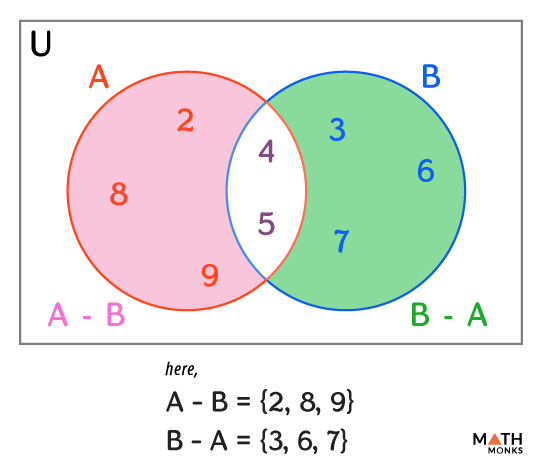
Let us consider two sets, A = {2, 4, 5, 8, 9} and B = {3, 4, 5, 6, 7}.

Case 1: A – B

Now, to find A – B, we follow the following steps:

Step 1: Finding the intersection of the sets A and B

A ∩ B 

= {2, 4, 5, 8, 9} ∩ {3, 4, 5, 6, 7}

= {4, 5}, the common elements of sets A and B.

Step 2: Eliminating the common elements from set A

A – (A ∩ B) 

= {2, 4, 5, 8, 9} – {4, 5}

= {2, 8, 9}

Step 3: Defining the new set A − B

Thus, A – B = {2, 8, 9}

Case 2: B – A

Similarly, B – A is a set obtained by removing the elements of A ∩ B from set B = B – (A ∩ B)

⇒ B – A = {3, 4, 5, 6, 7} – {4, 5} = {3, 6, 7}

Since A – B ≠ B – A, the difference between sets does not follow the commutative law. 

Now, representing both results with a Venn diagram, we get

Thus, A – B ≠ B – A

Two Disjoint Sets

If sets ‘A’ and ‘B’ are disjoint, they have no elements in common. Consequently, when we subtract set ‘B’ from set ‘A,’ there are no elements in ‘A’ to be subtracted or removed.

Mathematically, it can be expressed as

• A – B = A – (A ∩ B) = A
• B – A = B – (A ∩ B) =  B

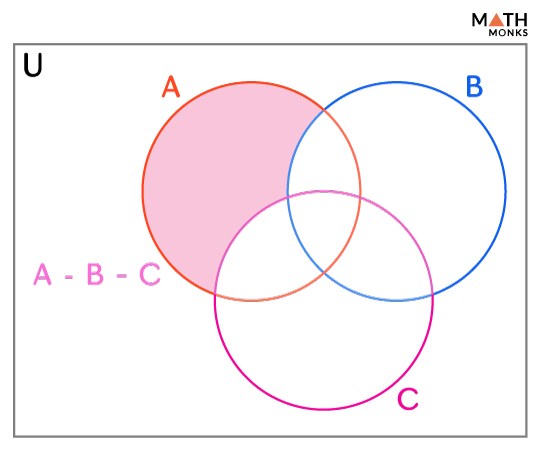
Difference of Three Sets

If ‘A,’ ‘B,’ and ‘C’ are three non-empty sets, then their difference represented by A – B – C is a set containing the elements of A that are not present in B and C.

Let A = {1, 2, 3, 4, 5}, B = {2, 3, 5, 6, 7}, and C = {3, 5, 7, 8}, then A – B – C is represented as shown.

Complement and Set Difference 

The complement of a set A, denoted by A’ or A^c, is the difference between the sets U and A, where ‘U’ is the universal set. 

Mathematically, it is expressed as 

A’ or A^c = U – A, which represents the set containing all elements of the universal set that are not present in set A.

For example, if A = {4, 9, 16, 25} and U = {0, 1, 4, 9, 16, 25, 36}

A’ = U – A = {0, 1, 4, 9, 16, 25, 36} – {4, 9, 16, 25} = {0, 1, 36}

Properties

• (A’)’ = A
• A ∪ A’ = U, where ‘U’ is the universal set.
• A ∩ A’ = ɸ, where ‘ɸ’ is the null set.
• De-Morgan’s Law: 

Intersection Over Union: (A ∪ B)^C = A^C ∩ B^C

Union Over Intersection: (A ∩ B)^C = A^C ∪ B^C

Set Difference and Complement

If ‘A’ and ‘B’ are two different sets:

• A – B = A ∩ B’ 
• A – A = ɸ
• A – ɸ = A
• ɸ – A = ɸ
• If A ∩ B = ɸ, then A – B = A 
• If A = B, then A – B = B – A = ɸ
• If A ⊂ B, then A – B = ɸ
• n(A △ B) = n(A – B) + n(B – A) or n(A △ B) = n(A U B) – n(A ∩ B)

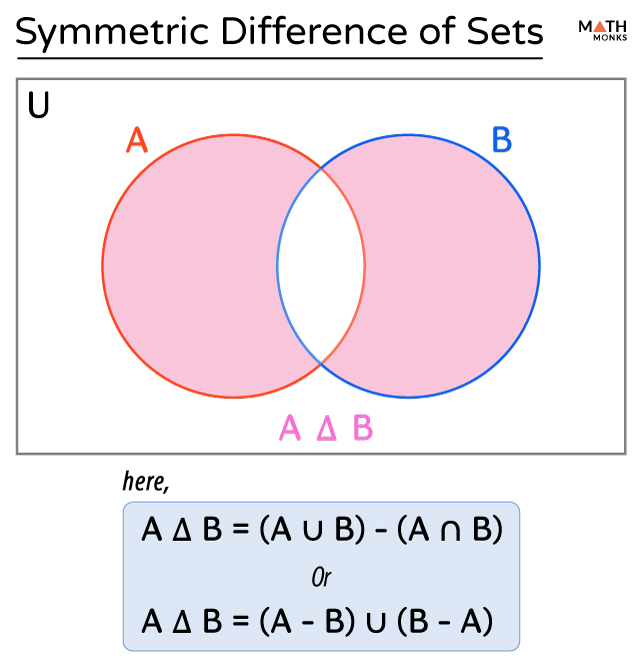
Symmetric Difference

The symmetric difference between two sets refers to a set that includes elements present in either set but not present in the intersection of ‘A’ and ‘B.’ It contains the elements found in sets A or B but not in both. 

Mathematically, it is represented by A △ B, or A ⊝ B, or A ⊕ B.

The symmetric difference in sets can also be calculated by the formula

A △ B = (A ∪ B) – (A ∩ B)

Or, A △ B = (A – B) ∪ (B – A)

Here is the Venn diagram of A Δ B.

Let us consider two sets, A = {9, 12, 15, 18} and B = {12, 18, 24, 30}

Now, finding the union of sets, we get

A ∪ B = {9, 12, 15, 18} ∪ {12, 18, 24, 30} = {9, 12, 15, 18, 24, 30}

Finding the intersection of sets, we get

A ∩ B = {9, 12, 15, 18} ∩ {12, 18, 24, 30} = {12, 18}

Now, the symmetric difference between sets A and B is

A △ B = (A ∪ B) – (A ∩ B)

⇒ A △ B = {9, 12, 15, 18, 24, 30} – {12, 18} = {9, 15, 24, 30}

Solved Examples