Table of Contents
Last modified on July 10th, 2024
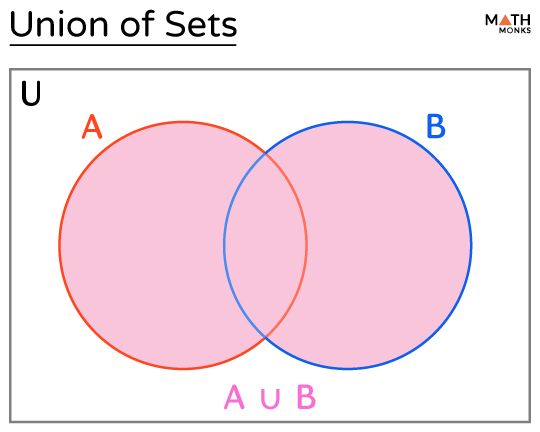
The union of two or more sets is a set that contains all the elements from the original sets without any repetition. If an element appears in any set, it will also appear in the union.
The union operation is denoted by the symbol ‘∪.’
The union of two sets, A and B, is a new set denoted by A ∪ B, which contains all the elements of sets A and B without repetition. It is read as ‘A union B.’
Let us consider an example.
If A = {1, 2, 3, 4, 5} and B = {6, 7, 10}
Then, A ∪ B = {1, 2, 3, 4, 5, 6, 7, 10}
The formula for the union of two sets (A union B ) is given in set builder notation as:
A ∪ B = {x | x ∈ A or x ∈ B}
This means x is an element of A ∪ B if and only if x is an element of A or x is an element of B.
In the Venn diagram, the shaded region illustrates the union of sets A and B. It covers all the elements from both sets, where U is the universal set.
Here, A ∪ B = {x | x ∈ A or x ∈ B}
For example,
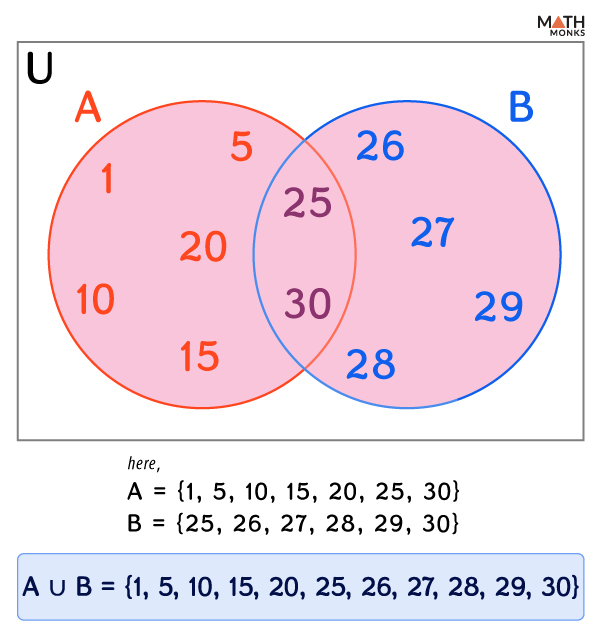
If set A = {1, 5, 10, 15, 20, 25, 30} and set B = {25, 26, 27, 28, 29, 30}, then the union of these two disjoint sets is
A ∪ B = {1, 5, 10, 15, 20, 25, 26, 27, 28, 29, 30}.
The result is thus a new set formed by combining all elements of the given sets, and its Venn diagram is shown:
If A and B are two sets, we can calculate the number of elements in their union set using the formula:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Here,
n(A ∪ B) = Cardinality of set A ∪ B
n(A) = Cardinality of set A
n(B) = Cardinality of set B
n(A ∩ B) = Cardinality of set A ∩ B
The union of two or more sets follows the commutative law. Thus, if A and B are two sets, then A ∪ B = B ∪ A
For example,
If A = {a, b} and B = {b, c, d}, then A ∪ B = {a, b, c, d} and B ∪ A = {b, c, d, a}
A ∪ B = B ∪ A
The union of three or more sets does not depend on how we group the sets. Thus, if A and B are two sets, then (A ∪ B) ∪ C = A ∪ (B ∪ C)
For example,
If A = {a, b}, B = {b, c, d}, and C = {c, d, e, f}, then
(A ∪ B) ∪ C = {a, b, c, d} ∪ {c, d, e, f} = {a, b, c, d, e, f}
A ∪ (B ∪ C) = {a, b} ∪ {b, c, d, e, f} = {a, b, c, d, e, f}
Thus, the associative law is satisfied.
If A, B, and C are three different sets, then according to the distributive law
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
The union of an empty set and a set A produces the set itself.
A ∪ ɸ = A
For example,
If A = {a, b} and ɸ = { }, then A ∪ ɸ = {a, b} ∪ { } = {a, b} = A
The union of a set A with itself is the set A.
A ∪ A = A
For example,
If A = {a, b}, then A ∪ A = {a, b} ∪ {a, b} = {a, b} = A
The union of a universal set U and its subset A is the universal set itself.
A ∪ U = U
For example,
If A = {a, b} and U = {a, b, p, q, s}, then A ∪ U = {a, b} ∪ {a, b, p, q, s} = {a, b, p, q, s} = U
If set A is a subset of set B, then the union of the two sets gives set B.
Using set notation,
If A ⊆ B, then A ∪ B = B
For example,
If A = {b} and B = {b, c, d}, then A ∪ B = {b, c, d} = B
Find the number of elements in the union of two sets, A and B, when n(A) = 6, n(B) = 5, and n(A ∩ B) = 2
As we know,
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Here,
n(A) = 6
n(B) = 5, and
n(A ∩ B) = 2
Thus, n(A ∪ B) = 6 + 5 – 2 = 9
If U is a universal set containing all the whole numbers until 10 and sets A and B are two subsets of U defined as A = {3, 7, 9} and B = {2, 4, 5, 6}, find A ∪ B and represent the resultant set in the Venn diagram.
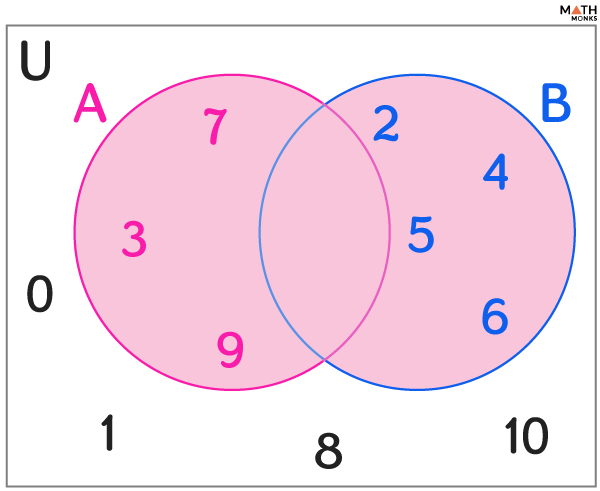
Here, U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10},
A = {3, 7, 9}, and
B = {2, 4, 5, 6}
Now, A ∪ B = {3, 7, 9} ∪ {2, 4, 5, 6} = {2, 3, 4, 5, 6, 7, 9}
Here is the Venn diagram of the set A ∪ B
Last modified on July 10th, 2024