Trigonometric functions like sine (sin) and cosine (cos) repeat themselves after an interval indefinitely and are thus called periodic functions.
While analyzing the nature of these functions, we analyze their graph for properties like amplitude, period, and frequency.
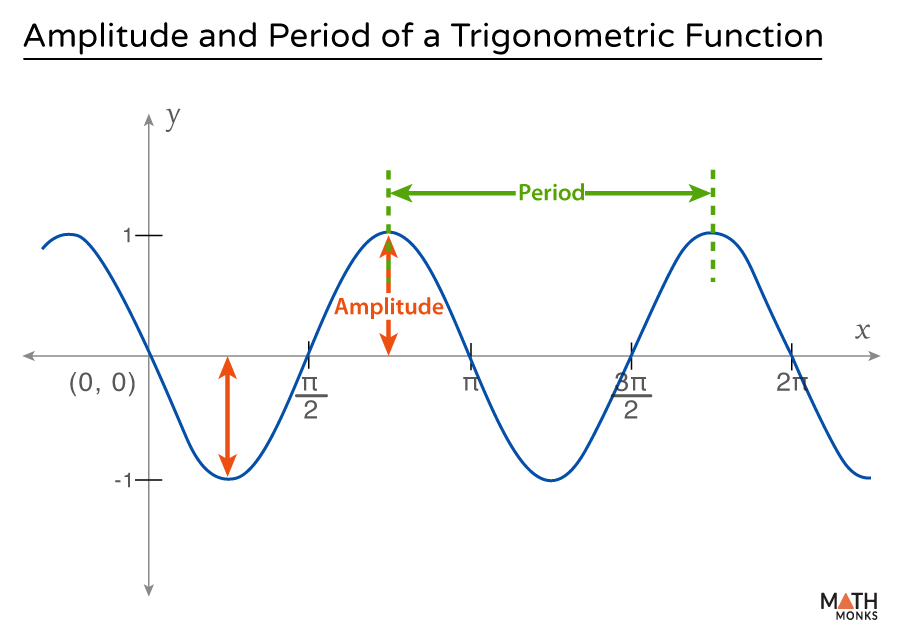
The amplitude represents the height of the curve, while the period measures the length of one complete cycle of the function.
Amplitude
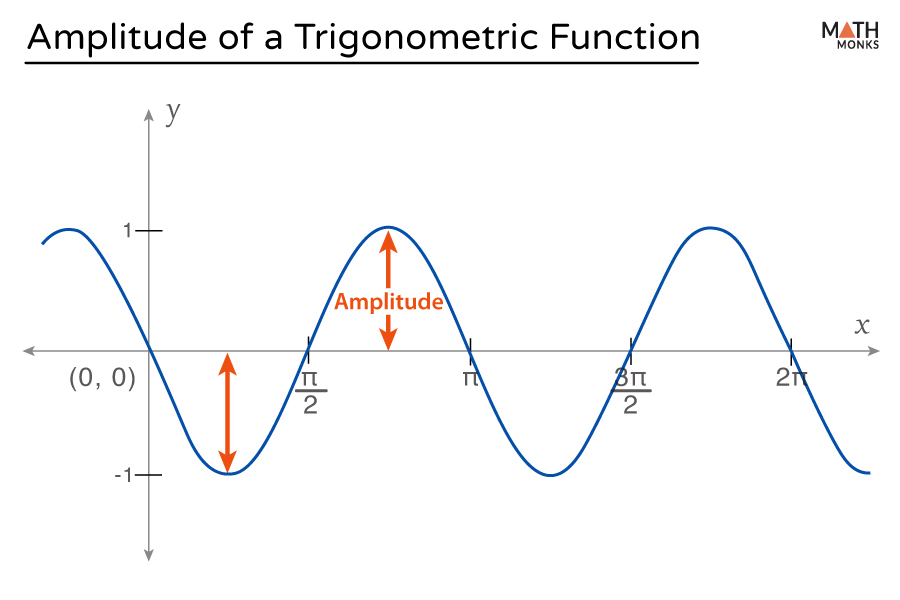
The amplitude of a trigonometric function refers to the height of its peaks (highest points) or the depth of its troughs (lowest points) relative to its midline, also known as the central axis or equilibrium position.
Thus, amplitude measures how far the function oscillates above and below its central axis.
The peaks and troughs of the function oscillate symmetrically around the midline. Thus,
- The larger amplitude leads to taller waves
- The smaller amplitude results in shorter waves
Formula
For a general trigonometric function
y = A sin x or y = A cos x,
The amplitude is |A|
Here,
A is the coefficient of the function, and the modulus gives its positive value.
Note: For the other trigonometric functions, the amplitude does not exist.
Finding Amplitude of y = 3 sin 4x
Given the function is: y = 3 sin 4x …..(i)
Step 1: Identifying the General Form of the Function
As we know, the general form of the function is y = A sin x …..(ii)
Step 2: Finding the Amplitude
Comparing the equations (i) and (ii), we get
The coefficient of cos x is A = 3
Thus, amplitude = |A| = |3| = 3
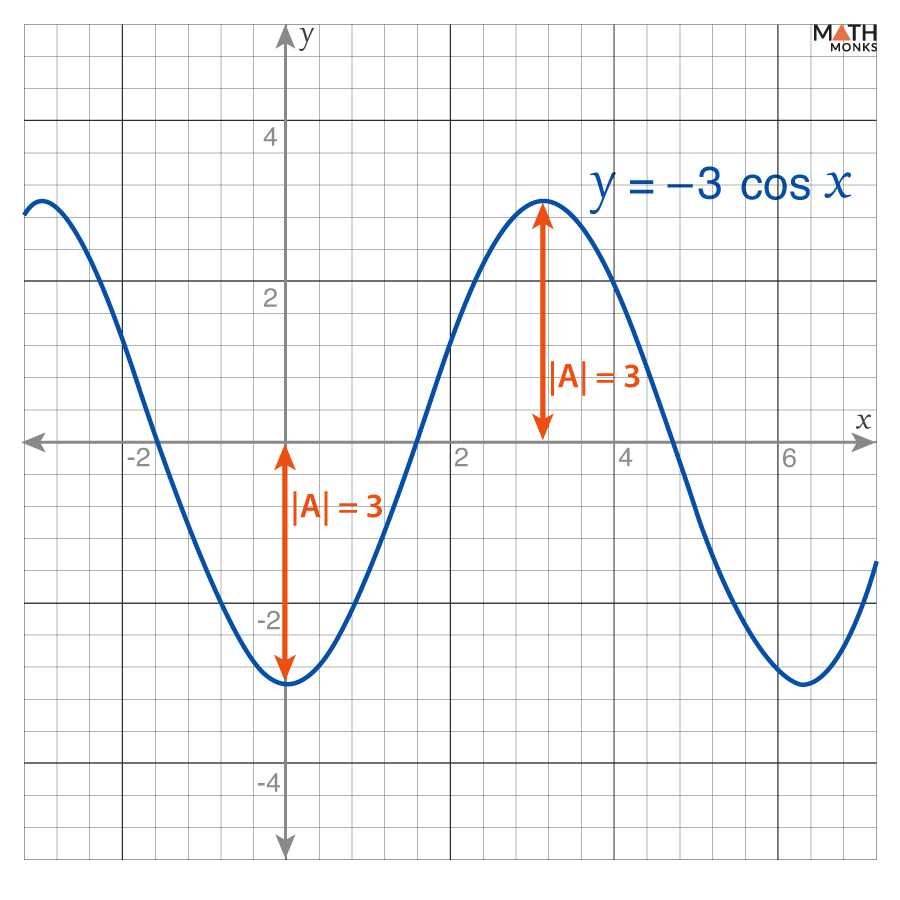
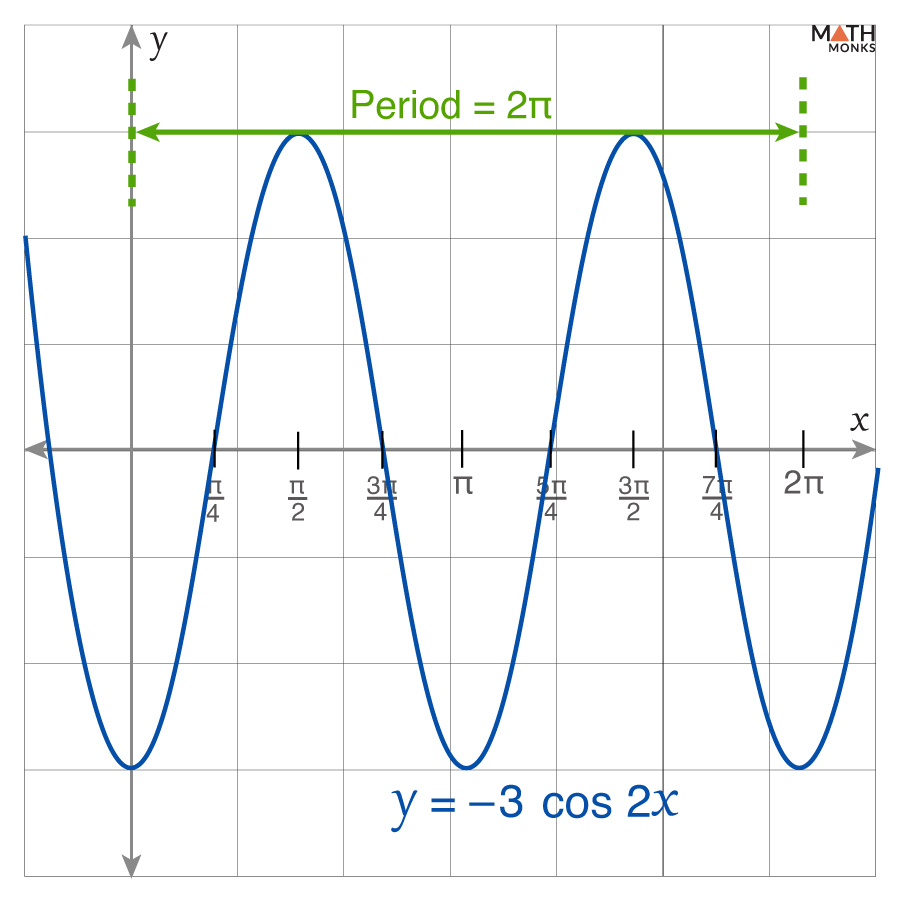
Finding Amplitude of y = -3 cos x
Given the function is: y = -3 cos x …..(i)
Step 1: Identifying the General Form of the Function
As we know, the general form of the function is y = A cos x …..(ii)
Step 2: Finding the Amplitude
Comparing the equations (i) and (ii), we get
The coefficient of cos x is A = -3
Thus, amplitude = |A| = |-3| = 3
Here, the graph oscillates between -3 and 3, with a reflection about the x-axis due to the negative coefficient.
Period
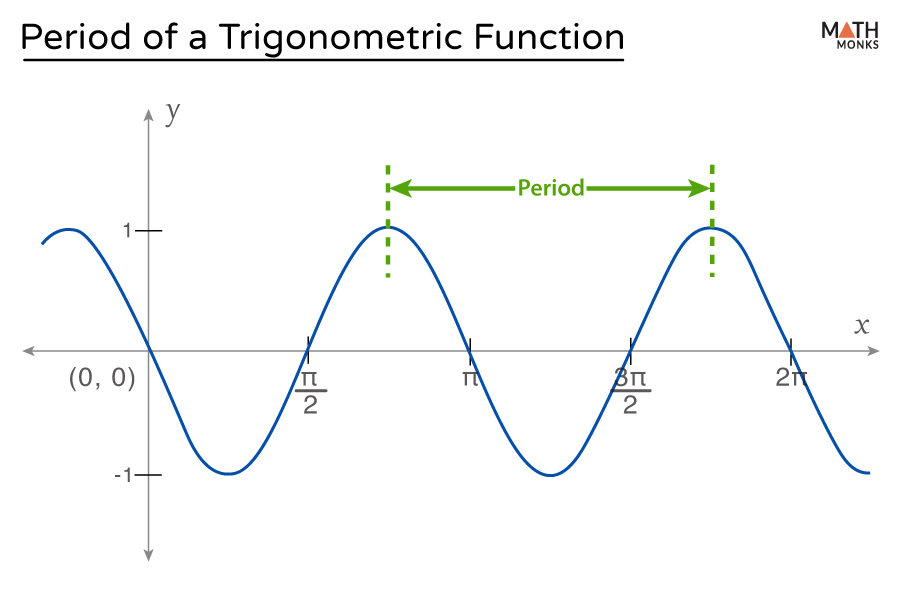
The period of a trigonometric function is the length of the interval required for the function to complete one full cycle.
For sine and cosine functions, the standard period is 2π, but it can be altered by a horizontal scaling factor.
Here,
- The closer the peaks and troughs, the shorter the period.
- Wider spacing indicates a longer period.
Formula
For a general trigonometric function
y = sin Bx or y = cos Bx
The period is ${\dfrac{\langle regular \ period\rangle }{\left| B\right| }}$
= ${\dfrac{2\pi }{\left| B\right| }}$
Here, B is the angular coefficient.
Similarly, the formula to find the period of the other 4 basic trigonometric functions is:
- Cosecant = ${\dfrac{2\pi }{\left| B\right| }}$
- Secant = ${\dfrac{2\pi }{\left| B\right| }}$
- Tangent = ${\dfrac{\pi }{\left| B\right| }}$
- Cotangent = ${\dfrac{\pi }{\left| B\right| }}$
Finding Period of y = 3 sin 4x
Given the function is y = 3 sin 4x …..(i)
Step 1: Identifying the General Form of the Function
As we know, the general form of the function is y = A sin Bx …..(ii)
Step 2: Finding the Period
Comparing the equations (i) and (ii), we get
The angular coefficient of sin Bx is B = 4
Since the regular period of the sine function is 2π
Thus, the period is ${\dfrac{2\pi }{\left| B\right| }}$ = ${\dfrac{2\pi }{\left| 4\right| }}$ = ${\dfrac{\pi }{2}}$
Finding Period of y = -3 cos 2x
Given the function is y = -3 cos 2x …..(i)
Step 1: Identifying the General Form of the Function
As we know, the general form of the function is y = A cos Bx …..(ii)
Step 2: Finding the Period
Comparing the equations (i) and (ii), we get
The angular coefficient of cos Bx is B = 2
Since the regular period of the cosine function is 2π
Thus, the period is ${\dfrac{2\pi }{\left| B\right| }}$ = ${\dfrac{2\pi }{\left| 2\right| }}$ = π
Solved Examples
![]() Find the amplitude of the function y = -5 sin 7x
Find the amplitude of the function y = -5 sin 7x
Solution:
![]()
Given, y = -5 sin 7x …..(i)
As we know, the general form of the sine function is y = A sin Bx …..(ii)
Comparing equations (i) and (ii), we get
A = -5
Thus, the amplitude is |A| = |-5| = 5
![]() Find the amplitude and period of the function ${y=-4\cos \dfrac{x}{2}}$
Find the amplitude and period of the function ${y=-4\cos \dfrac{x}{2}}$
Solution:
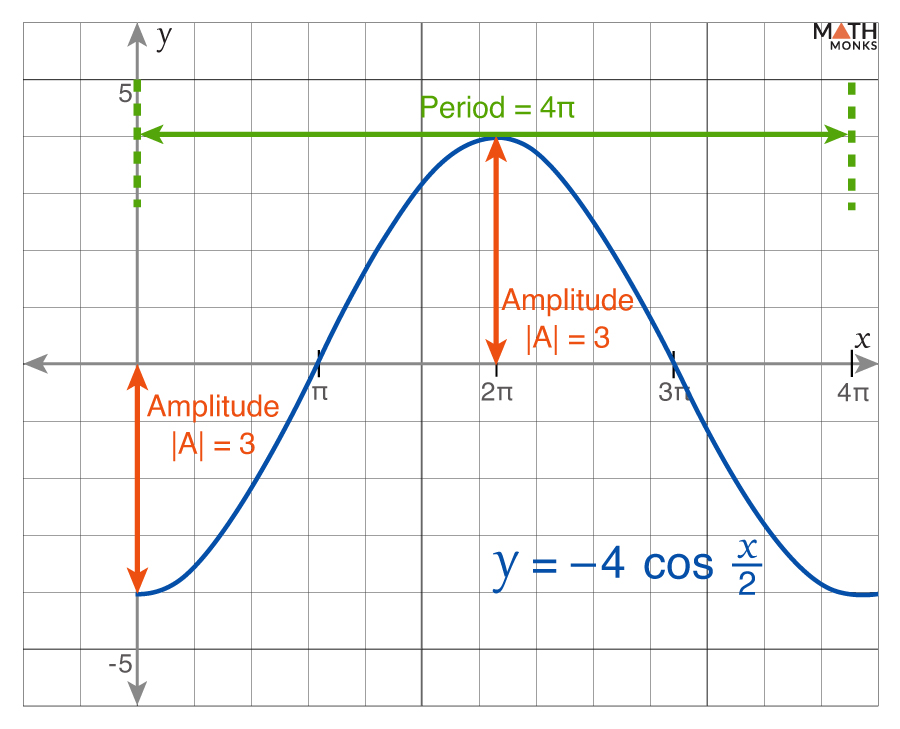
Given, ${y=-4\cos \dfrac{x}{2}}$ …..(i)
As we know, the general form of the cosine function is y = A cos Bx …..(ii)
Comparing equations (i) and (ii), we get
A = -4
B = ${\dfrac{1}{2}}$
Thus, the amplitude is |A| = |-4| = 4
Since the regular period of the cosine function is 2π
Thus, the period is ${\dfrac{\langle regular \ period\rangle }{\left| B\right| }}$
= ${\dfrac{2\pi }{\left| B\right| }}$
= ${\dfrac{2\pi }{\dfrac{1}{2}}}$
= ${4\pi}$
Thus, the amplitude is 4, and the period is 4π
![]() Find the period of the tangent function y = 2 tan 3x
Find the period of the tangent function y = 2 tan 3x
Solution:
![]()
Given, y = 2 tan 3x …..(i)
As we know, the general form of the tangent function is y = A tan Bx …..(ii)
Comparing equations (i) and (ii), we get
B = 3
Since the regular period of the tangent function is π
Thus, the period is ${\dfrac{\langle regular \ period\rangle }{\left| B\right| }}$
= ${\dfrac{\pi }{\left| B\right| }}$
= ${\dfrac{\pi }{\left| 3\right| }}$
= ${\dfrac{\pi }{3}}$