Domain refers to all possible input values (usually represented by x) for which a function is true, while range represents all possible output values (usually represented by y) the function can produce.
For trigonometric functions, the domain and range are closely related to their periodic nature and the unit circle. They define the properties of the functions.
Sine (y = sin x)
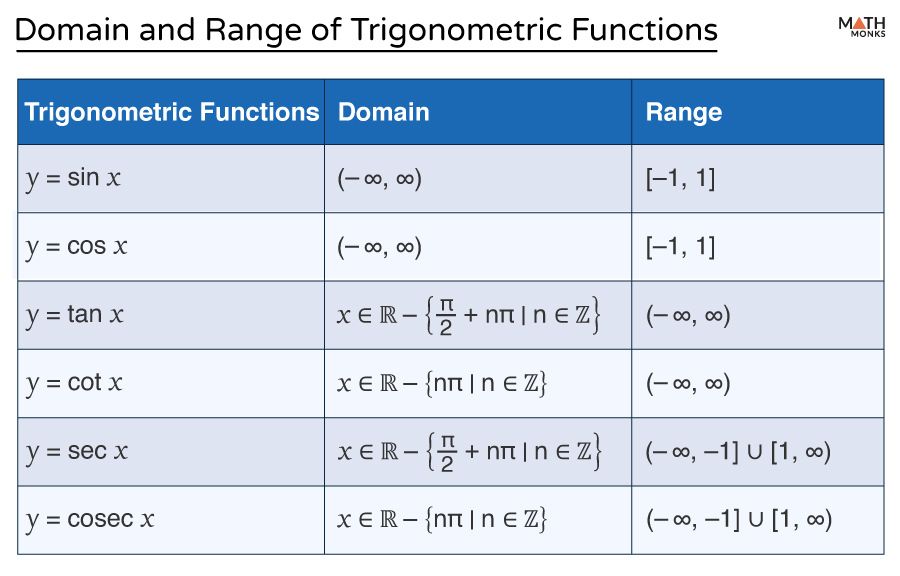
Since there is no restriction on the input x, the sine function holds true for all real numbers. Its output ranges between -1 and 1.
- Domain: (-∞, ∞)
- Range: [-1, 1]
Cosine (y = cos x)
Like sine, cosine is defined for all real numbers. Its output also oscillates between -1 and 1.
- Domain: (-∞, ∞)
- Range: [-1, 1]
Tangent (y = tan x)
The tangent function is undefined at odd multiples of ${\dfrac{\pi }{2}}$ because the cosine of those angles is 0 (division by zero is undefined). Its output takes all real values.
- Domain: ${x\in \mathbb{R} -\left\{ \dfrac{\pi }{2}+n\pi | n\in \mathbb{Z} \right\}}$
- Range: (-∞, ∞)
Cosecant (y = cosec x)
For being the inverse of the sine function, the cosecant function is undefined at integer multiples of π. Its range is given below:
- Domain: ${x\in \mathbb{R} -\left\{ n\pi | n\in \mathbb{Z} \right\}}$
- Range = (-∞, -1] ∪ [1, ∞)
Secant (y = sec x)
For being the inverse of the cosine function, the secant function is undefined at odd multiples of ${\dfrac{\pi }{2}}$. Its range is given below:
- Domain: ${x\in \mathbb{R} -\left\{ \dfrac{\pi }{2}+n\pi | n\in \mathbb{Z} \right\}}$
- Range: (-∞, -1] ∪ [1, ∞)
Cotangent (y = cot x)
For being the inverse of the tangent function, the cotangent function is undefined at integer multiples of π. Its output takes all real values.
- Domain = ${x\in \mathbb{R} -\left\{ n\pi | n\in \mathbb{Z} \right\}}$
- Range = (-∞, ∞)
Here is a summary table for the domain and range of all six trigonometric functions:
Graphing
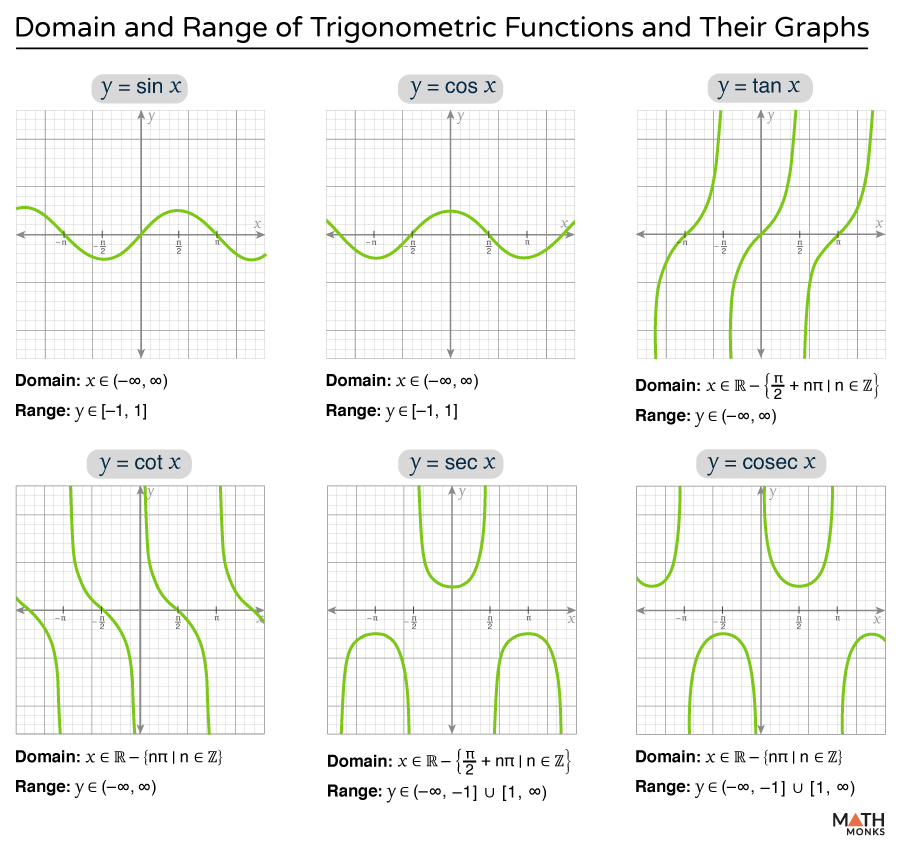
Here are the graphs of the six trigonometric functions:
In the graphs, the x-and-y-axis represents the domain and range of the functions, respectively. Thus, we can find the domain and range of these functions from their corresponding graphs.
How To Find Domain and Range
Let us find the domain and range of the function y = 3 cos x – 1
Step 1: Studying the Parent Function
As we know, the domain of the cosine function is (-∞, ∞), and the range is [-1, 1]
-∞ < x < ∞ …..(i)
-1 ≤ cos x ≤ 1 …..(ii)
Step 2: Transforming the Range of the Parent Function
On multiplying (ii) by 3, we get
-3 ≤ 3 cos x ≤ 3
Subtracting 1 from both sides, we get
⇒ -3 – 1 ≤ 3 cos x – 1 ≤ 3 – 1
⇒ -4 ≤ 3 cos x – 1 ≤ 2
⇒ -4 ≤ y ≤ 2 …..(iii)
Step 3: Determining the Domain and Range
Thus, from (i) and (iii), we get
The domain of the function is (-∞, ∞)
The range of the function is [-4, 2]
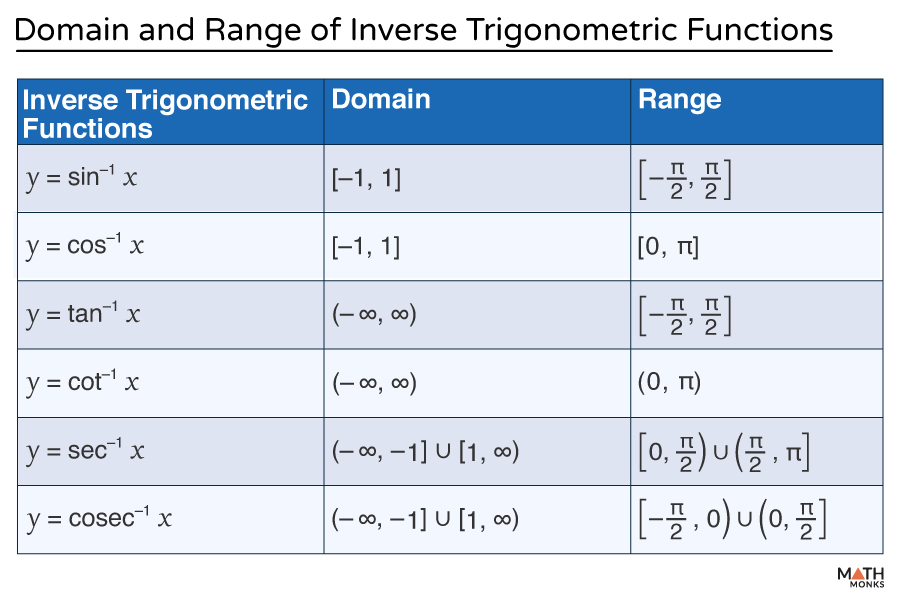
For Inverse Trigonometric Functions
Here is the table representing the domain and range of the inverse of the six basic trigonometric functions:
Solved Examples
![]()
Find the domain and range of the function: y = sec 2x + 4
Solution:
![]()
As we know, the domain and the range of the secant function (sec x) are:
Domain = ${x\in \mathbb{R} -\left\{ \dfrac{\pi }{2}+n\pi | n\in \mathbb{Z} \right\}}$ …..(i)
Range = (-∞, -1] ∪ [1, ∞) …..(ii)
Here, the function is y = sec 2x + 4
From (i), we get
${2x=\dfrac{\pi }{2}+n\pi}$, n ∈ ℤ
⇒ ${x=\dfrac{\pi }{4}+\dfrac{n\pi }{2}}$
Thus, the domain is ${x\in \mathbb{R} -\left\{ \dfrac{\pi }{4}+\dfrac{n\pi }{2} | n\in \mathbb{Z} \right\}}$
Now, from (ii), we get
sec 2x ∈ (-∞, -1] ∪ [1, ∞)
Adding 4 to both sides, we get
⇒ sec 2x + 4 ∈ (-∞, 3] ∪ [5, ∞)
Thus, the range is (-∞, 3] ∪ [5, ∞)
![]()
Find the domain and range of f(x) = tan-1 (2x – 1)
Solution:
![]()
As we know, the domain of tan-1 x is (-∞,∞), and the range of tan-1 x is ${\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right)}$
The argument of the function is 2x – 1, which is a linear expression. Since there are no restrictions on x, 2x – 1 can take any real value.
Thus, the domain of f(x) is (-∞,∞)
Since the range of tan-1 x depends only on the output of the function, the transformation 2x – 1 does not affect the range of the inverse tangent function.
Thus, the range of f(x) is ${\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right)}$
