Trigonometric functions, like all mathematical functions, can be classified as even, odd, both even and odd, or neither. These functions are categorized based on their symmetry.
A trigonometric function f(x) is:
- Even if the function is symmetric about the y-axis, f(-x) = f(x). For example, f(x) = x2, where f(-x) = (-x)2 = x2
- Odd if the function is symmetric about the origin; f(−x) = −f(x). For example, f(x) = x3, where f(-x) = (-x)3 = -x3
Sometimes, trigonometric functions can be even or odd at the same time or neither.
- Both even and odd if f(-x) = f(x) and f(-x) = -f(x) for all x in the domain. For example, f(x) = f(-x) = 0
- Neither even nor odd if the function does not satisfy f(-x) = f(x) or f(-x) = -f(x) for at least one value of x in its domain. For example, f(x) = x3 + x2 – 2, where f(-x) = (-x)3 + (-x)2 – 2 = -x3 + x2 – 2 which is neither equal to f(x) nor -f(x).
The following table lists the even and odd trigonometric functions:
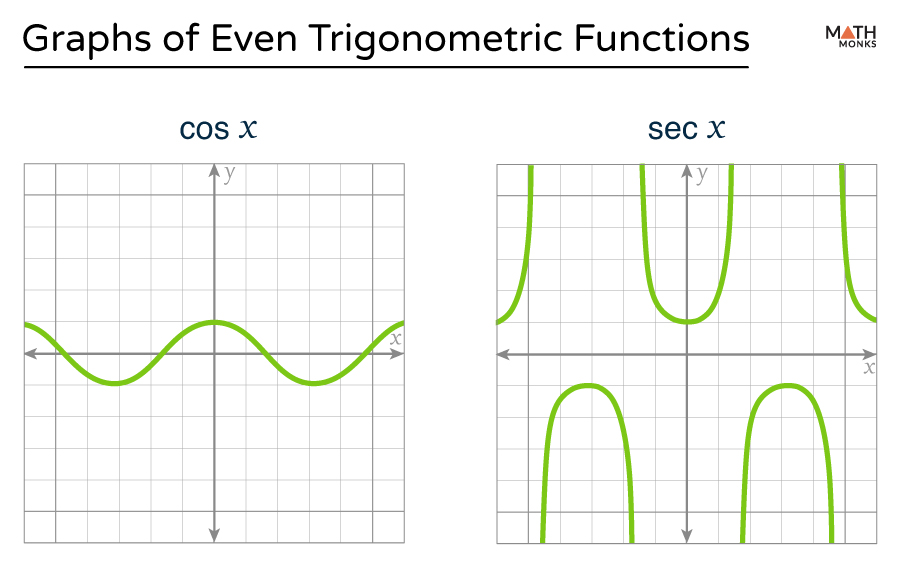
Even Functions
Cosine and secant functions are symmetric about the y-axis. Mathematically,
- If f(x) = cos x, then f(-x) = cos(-x) = cos x.
- If f(x) = sec(x), then f(-x) = sec(-x) = sec x.
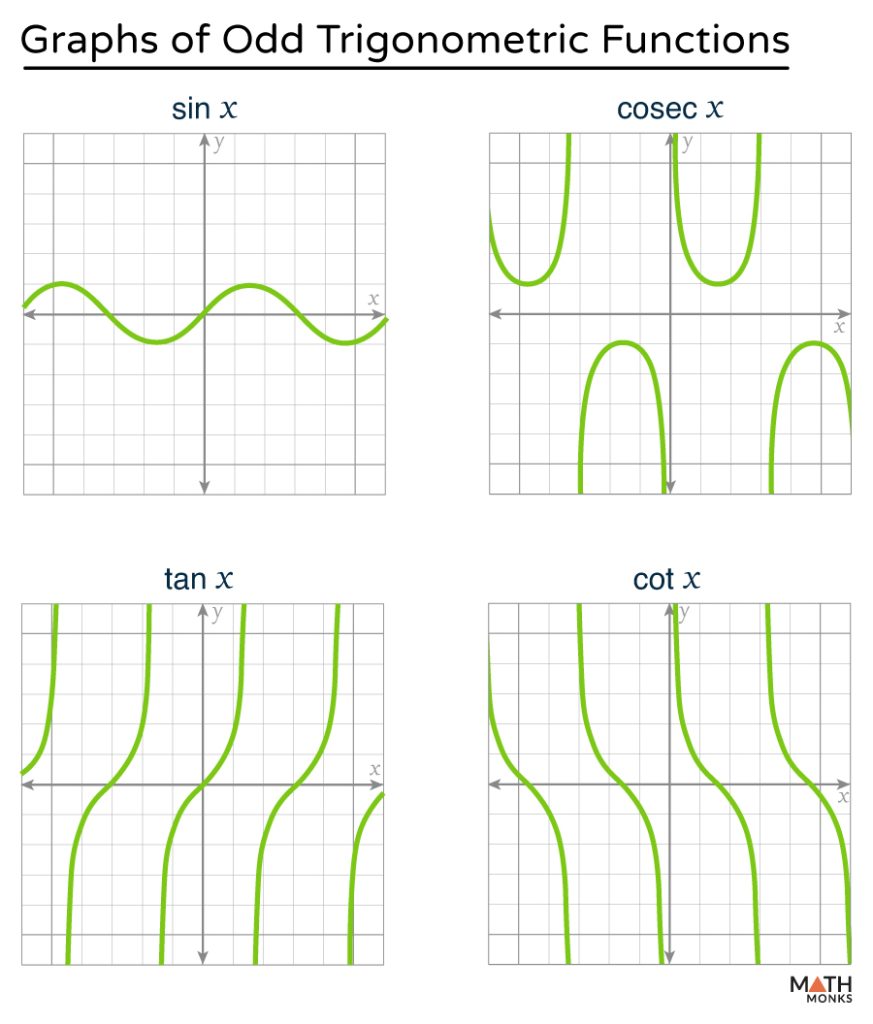
Odd Functions
Sine, tangent, and their reciprocals (cosecant and cotangent) are symmetric about the origin. Mathematically,
- If f(x) = sin x, then f(-x) = sin(-x) = -sin x.
- If f(x) = cosec x, then f(-x) = cosec(-x) = -cosec x.
- If f(x) = tan x, then f(-x) = tan(-x) = -tan x.
- If f(x) = cot x, then f(-x) = cot(-x) = -cot x.
Graphing
Even Functions
Since the graphs of even trigonometric functions are symmetric with respect to the y-axis, for any two opposite values of x, the function values remain identical.
Odd Functions
The graphs of odd trigonometric functions are symmetric with respect to the origin. For any two opposite values of x, the function values have the same magnitude but opposite signs.
Proofs
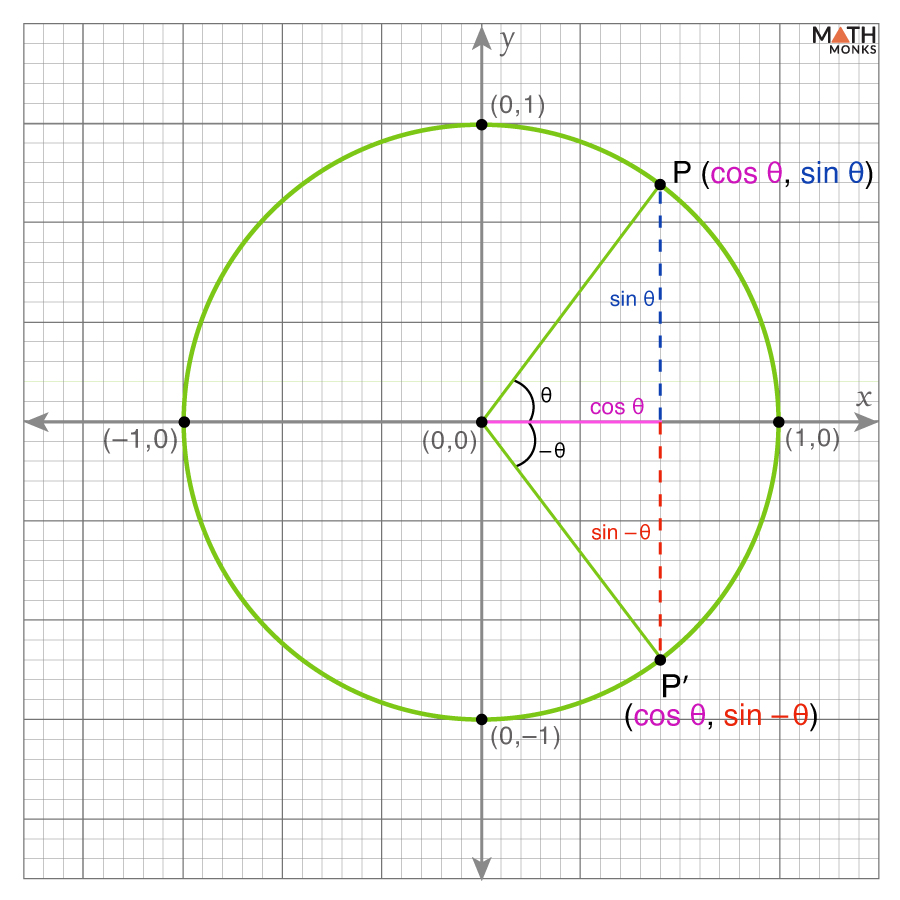
Let us now prove why the above-discussed trigonometric functions are even or odd. To prove this, we will use a unit circle.
The Sine Function is Odd
In the unit circle, the sine of an angle (let θ) corresponds to the y-coordinate of the point where the end side of the angle intersects the circle.
For angle -θ, which is the reflection of θ across the x-axis, the y-coordinate becomes the negative of that for θ.
Thus, sin(-θ) = -sin θ
Since sin(-θ) = -sin θ, the sine function is odd.
The Cosine Function is Even
In the unit circle, the cosine of an angle (let θ) corresponds to the x-coordinate of the point where the end side of the angle intersects the circle.
Reflecting θ across the x-axis to get -θ does not change the x-coordinate.
Thus, cos(-θ) = cos θ
Since cos(-θ) = cos θ, the cosine function is even.
The Tangent Function is Odd
By the definition of the tangent function,
${\tan \theta =\dfrac{\sin \theta }{\cos \theta }}$
From the properties of sine and cosine, we get
${\tan \left( -\theta \right) =\dfrac{\sin \left( -\theta \right) }{\cos \left( -\theta \right) }}$
= ${\dfrac{-\sin \theta }{\cos \theta }}$
= ${-\tan \theta}$
Since tan(-θ) = -tan θ, the cosine function is odd.
The Cotangent Function is Odd
By the definition of the cotangent function,
${\cot \theta =\dfrac{\cos \theta }{\sin \theta }}$
From the properties of sine and cosine, we get
${\cot \left( -\theta \right) =\dfrac{\cos \left( -\theta \right) }{\sin \left( -\theta \right) }}$
= ${\dfrac{\cos \theta }{-\sin \theta }}$
= ${-\cot \theta}$
Since cot(-θ) = -cot θ, the cosine function is odd.
The Cosecant Function is Odd
By the definition of the cosecant function,
${\text{cosec}\, \theta =\dfrac{1}{\sin \theta }}$
By using the property of sine, we get
${\text{cosec}\, \left( -\theta \right) =\dfrac{1}{\sin \left( -\theta \right) }}$
= ${\dfrac{1}{-\sin \theta }}$
= ${-\text{cosec}\, \theta }$
Since cosec(-θ) = -cosec θ, the cosine function is odd.
The Secant Function is Even
By the definition of the cosecant function,
${\sec \theta =\dfrac{1}{\cos \theta }}$
By using the property of cosine, we get
${\sec \left( -\theta \right) =\dfrac{1}{\cos \left( -\theta \right) }}$
= ${\dfrac{1}{\cos \theta }}$
= ${\sec \theta }$
Since sec(-θ) = sec θ, the cosine function is even.
Properties
Addition
- The sum of two even functions gives an even function, whereas the sum of two odd functions results in an odd function.
- The sum of an even and an odd function gives neither an even nor an odd function unless one of them is a zero function.
Subtraction
The difference between two even functions gives an even function, whereas the difference between two odd functions results in an odd function.
Multiplication
- The product of two even functions gives an even function, and the product of two odd functions results in an even function.
- The product of an even and an odd function gives an odd function.
Division
- The quotient of two even functions gives an even function, and the quotient of two odd functions results in an even function.
- The quotient of an even and an odd function gives an odd function.
- The quotient of an even and an odd function gives an odd function.
Composition
- The composition of any two even functions gives an even function, whereas the composition of any two odd functions results in an odd function.
- The composition of an even and an odd function gives an even function.
Integration
- If the function is even and the interval is [-a, a], then ${\int ^{a}_{-a}f\left( x\right) dx=2\int ^{a}_{0}f\left( x\right) dx}$
- If the function is odd and the interval is [-a, a], then ${\int ^{a}_{-a}f\left( x\right) dx=0}$
How To Find Even or Odd Functions
Now, let us find whether the function f(x) = cosec x – cot x is even, odd, or neither.
Step 1: Substituting -x into f(x)
f(-x) = cosec(-x) – cot(-x)
Since cosec(-x) = -cosec x and cot(-x) = -cot x
Here, f(-x) = -cosec x – (-cot x) = -cosec x + cot x
Step 2: Comparing f(x) and f(-x)
f(x) = cosec x – cot x
f(-x) = -cosec x + cot x = -(cosec x – cot x)
Now, comparing f(x) and f(-x), we get
f(-x) = -f(x)
Thus, the function is odd.
Solved Examples
![]() Find whether the function g(x) = x3 sin2 x cos x is even, odd, or neither.
Find whether the function g(x) = x3 sin2 x cos x is even, odd, or neither.
Solution:
![]()
Given, g(x) = x3 sin2 x cos x …..(i)
Substituting -x into g(x),
g(-x) = (-x)3 sin2(-x) cos(-x)
Since the sine function is odd and the cosine function is even.
Here, (-x)3 = -x3, sin2(-x) = (sin(-x))2 = (-sin x)2 = sin2 x, and cos(-x) = cos x
Now, g(-x) = -x3 sin2 x cos x …..(ii)
Comparing equations (i) and (ii), we get
g(-x) = -g(x)
Thus, g(x) is an odd function.
![]() Determine whether k(x) = tan3 x – cot x even, odd, or neither.
Determine whether k(x) = tan3 x – cot x even, odd, or neither.
Solution:
![]()
Given, k(x) = tan3 x – cot x …..(i)
Substituting -x into k(x),
k(-x) = tan3(-x) – cot(-x)
Since the tangent and cotangent functions are odd.
Here, tan3(-x) = (tan(-x))3 = -tan3 x and cot(-x) = -cot x
Now, k(-x) = -tan3 x – (-cot x) = -tan3 x + cot x = -(tan3 x – cot x) …..(ii)
Comparing equations (i) and (ii), we get
k(-x) = -k(x)
Thus, k(x) is an odd function.
![]() Verify whether the function n(x) = sin x tan x is an even.
Verify whether the function n(x) = sin x tan x is an even.
Solution:
![]()
Given, n(x) = sin x tan x …..(i)
Substituting -x into n(x),
n(-x) = sin(-x) tan(-x)
Since the sine and tangent functions are odd.
Here, sin(-x) = -sin x and tan(-x) = -tan x
Now, n(-x) = (-sin x)(-tan x) = sin x tan x …..(ii)
Comparing equations (i) and (ii), we get
n(-x) = n(x)
Thus, n(x) is an even function.
![]() Which of the following trigonometric functions is an odd function, and why?
Which of the following trigonometric functions is an odd function, and why?
a) sin x
b) cos x
c) cot2 x
Solution:
![]()
Here, option a) sin x is an odd function as sin(-x) = -sin x