Trigonometric functions, being periodic by nature, repeat their values over specific intervals. This periodicity can be easily represented by graphing them. Each of the six trigonometric functions, sine, cosine, tangent, cotangent, secant, and cosecant, and their inverses have unique properties, including amplitude, period, phase shift, and vertical shift, which influence their graphs.
For graphing these functions, it is important to identify their fundamental properties and domains. Typically, the domain restrictions are either the interval ${\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]}$ or [0, π], depending on the function.
Graphing trigonometric functions is a visual way to explore their behavior, interpret their periodicity, and apply their principles to solve real-world problems.
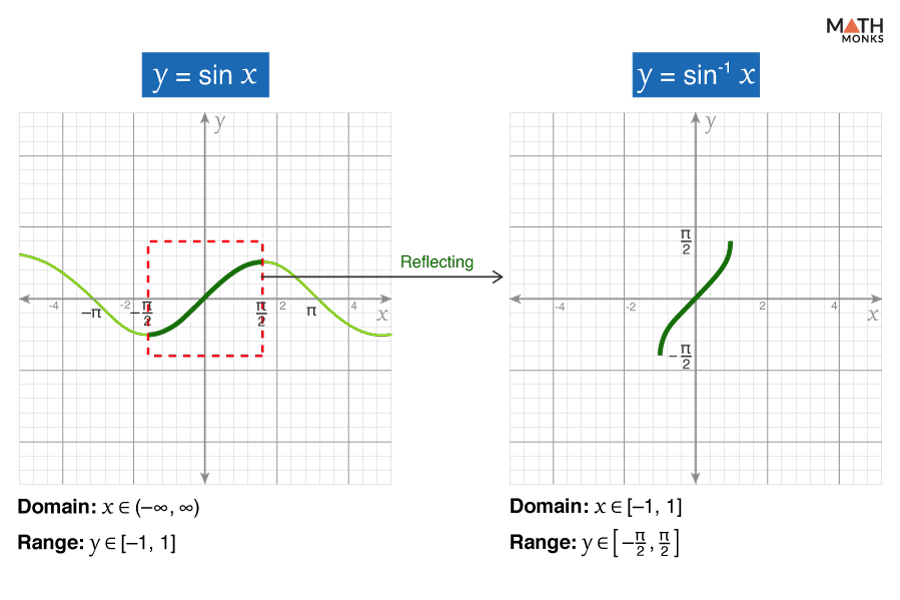
Arcsine (y = sin-1 x)
The sine function oscillates between -1 and 1, which is thus an ideal starting point for understanding periodic behavior. The arcsine function is the inverse of the sine function (sin x) and is represented as sin-1 x or arcsin (x).
To graph sin-1 x, we first restrict the domain of the sine function to ${\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]}$ and then reflect the restricted graph across the line y = x
The graph of sin-1 x intersects the coordinate axes at the origin (0, 0). It is symmetric with respect to the rotation around (0, 0).
Here,
- Domain: x ∈ [-1, 1]
- Range: y ∈ ${\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]}$
- X-Intercept: x = 0
- Y-Intercept: y = 0
- Minima: ${\left( -1,-\dfrac{\pi }{2}\right)}$
- Maxima: ${\left( 1,\dfrac{\pi }{2}\right)}$
- Inflection Points: (0, 0)
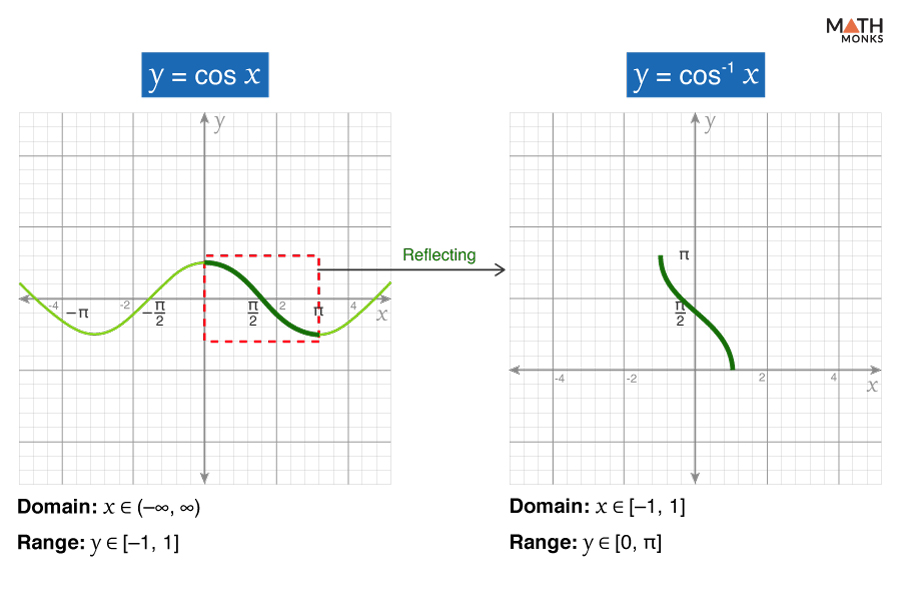
Arccosine (y = cos-1 x)
The arccosine function is the inverse of the cosine function (cosx) and is represented as cos-1 x or arccos (x).
To graph cos-1 x, we first restrict the domain of the cosine function to [0, π] and then reflect the restricted graph across the line y = x
The graph of cos-1 x intersects the coordinate axes at ${\left( 1,\dfrac{\pi }{2}\right)}$. It has no symmetry, is neither an even nor an odd function, and is strictly decreasing within the interval (-1, 1).
Here,
- Domain: x ∈ [-1, 1]
- Range: y ∈ [0, π]
- X-Intercept: x = 1
- Y-Intercept: y = ${\dfrac{\pi }{2}}$
- Minima: (1, 0)
- Maxima: (-1, π)
- Inflection Points: ${\left( 0,\dfrac{\pi }{2}\right)}$
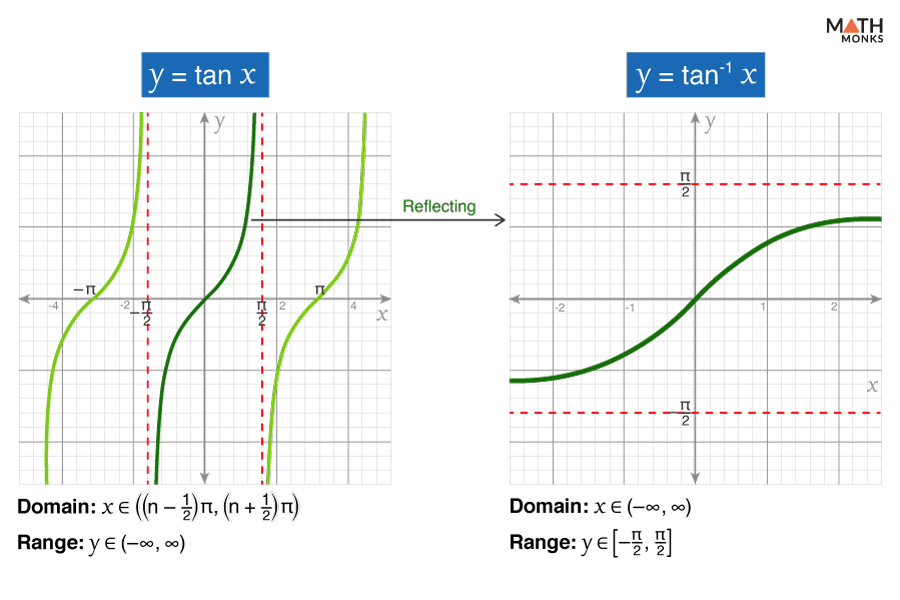
Arctangent (y = tan-1 x)
The arctangent function is the inverse of the tangent function (tanx) and is represented as tan-1 x or arctan (x).
To graph tan-1 x, we first restrict the domain of the tangent function to ${\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]}$ and then reflect the restricted graph across the line y = x
The graph of tan-1 x intersects the coordinate axes at the origin (0, 0). It is strictly increasing over (-∞, ∞) and has odd symmetry about the origin.
Here,
- Domain: x ∈ ℝ
- Range: y ∈ ${\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right)}$
- X-Intercept: x = 0
- Y-Intercept: y = 0
- Minima: It has no minima points
- Maxima: It has no maxima points
- Inflection Points: (0, 0)
- Asymptotes: y = ${\dfrac{\pi }{2}}$ and y = ${-\dfrac{\pi }{2}}$
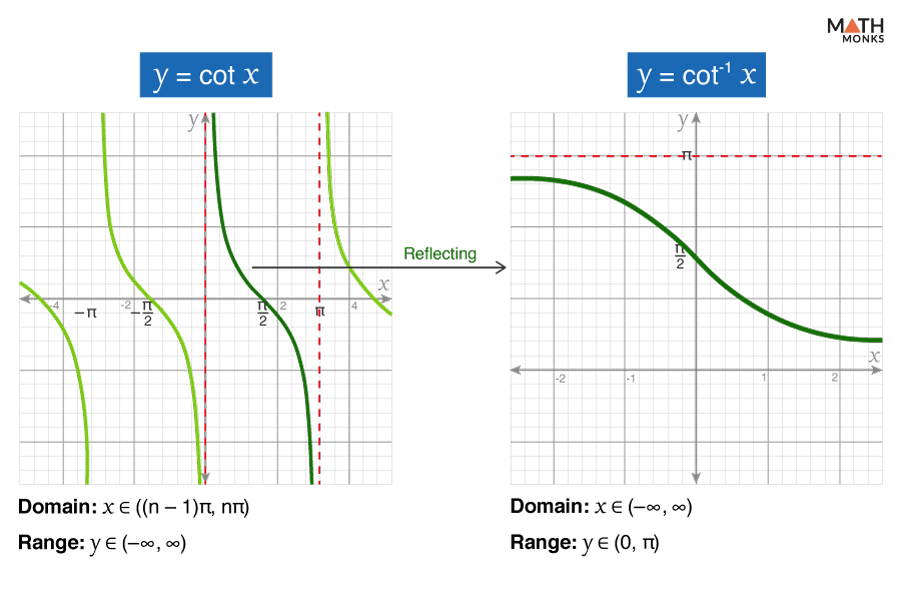
Arccotangent (y = cot-1 x)
The arccotangent function is the inverse of the cotangent function (cotx) and is represented as cot-1 x or arccot (x).
To graph cot-1 x, we first restrict the domain of the cotangent function to [0, π] and then reflect the restricted graph across the line y = x
The graph of cot-1 x intersects the y-axis at ${\left( 0,\dfrac{\pi }{2}\right)}$. It is neither an even nor odd function and strictly decreases over the interval (-∞, ∞).
Here,
- Domain: x ∈ ℝ
- Range: y ∈ (0, π)
- X-Intercept: It does not exist since the graph does not pass through the x-axis.
- Y-Intercept: y = ${\dfrac{\pi }{2}}$
- Minima: It has no minima points
- Maxima: It has no maxima points
- Inflection Points: It has no inflection points.
- Asymptotes: y = 0 and y = π
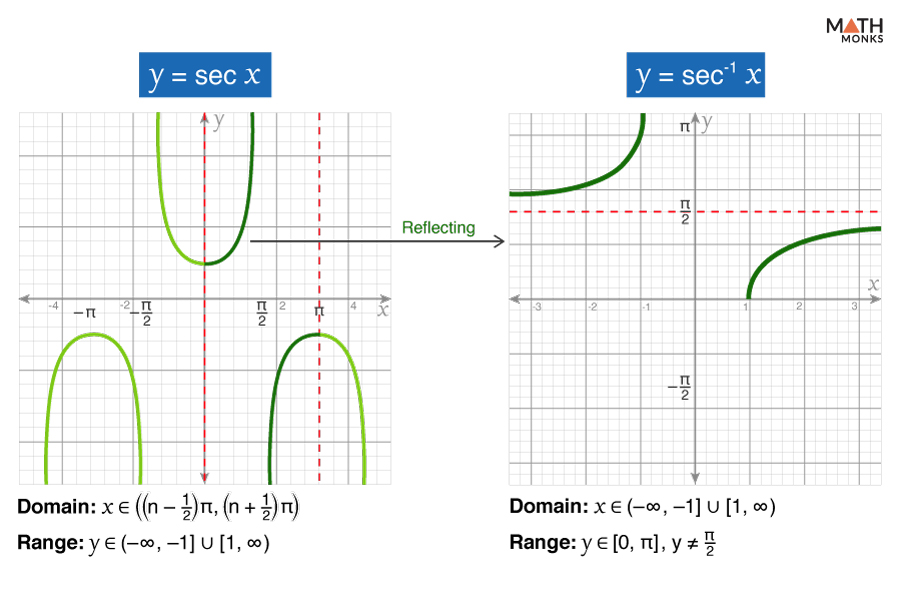
Arcsecant (y = sec-1 x)
The arcsecant function is the inverse of the secant function (sec x) and is represented as sec-1 x or arcsec (x).
To graph sec-1 x, we first restrict the domain of the secant function to [0, π] and then reflect the restricted graph across the line y = x
The graph of sec-1 x is discontinuous, indicating it does not intersect the y-axis. It is neither an even nor an odd function and strictly increases over the interval (-∞, ∞), except at points of discontinuity.
Here,
- Domain: x ∈ (-∞, -1] ∪ [1, ∞)
- Range: y ∈ ${[ 0,\dfrac{\pi }{2}) \cup ( \dfrac{\pi }{2},\pi ]}$
- X-Intercept: x = 1
- Y-Intercept: It does not exist since the graph does not pass through the y-axis.
- Minima: (1, 0)
- Maxima: (-1, π)
- Inflection Points: It has no inflection points.
- Asymptotes: y = ${\dfrac{\pi }{2}}$
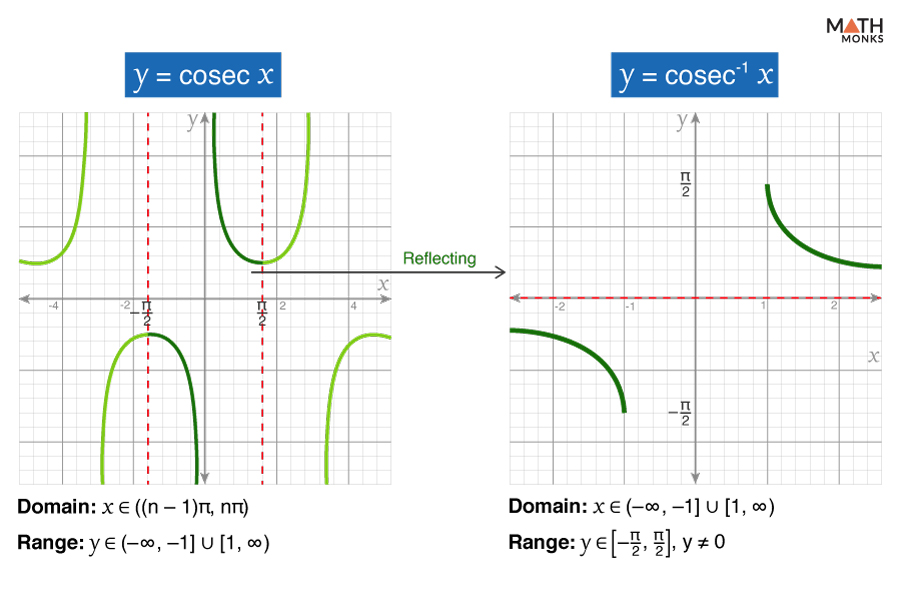
Arccosecant (y = cosec-1 x)
The arccosecant function is the inverse of the cosecant function (cosec x) and is represented as cosec-1 x or arccosec x.
To graph cosec-1 x, we first restrict the domain of the cosecant function to ${\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]}$ and then reflect the restricted graph across the line y = x
The graph of cosec-1 x is discontinuous, indicating it does not intersect the coordinate axes. It is an odd function that decreases strictly within its domain.
Here,
- Domain: x ∈ (-∞, -1] ∪ [1, ∞)
- Range: y ∈ ${[ -\dfrac{\pi }{2},0) \cup ( 0,\dfrac{\pi }{2} ]}$
- X-Intercept: It does not exist since the graph does not pass through the x-axis.
- Y-Intercept: It does not exist since the graph does not pass through the y-axis.
- Minima: ${\left( -1,-\dfrac{\pi }{2}\right)}$
- Maxima: ${\left( 1,\dfrac{\pi }{2}\right)}$
- Inflection Points: It has no inflection points.
- Asymptotes: y = 0
Summary
Here is a summary of the graphs of the six inverse functions.