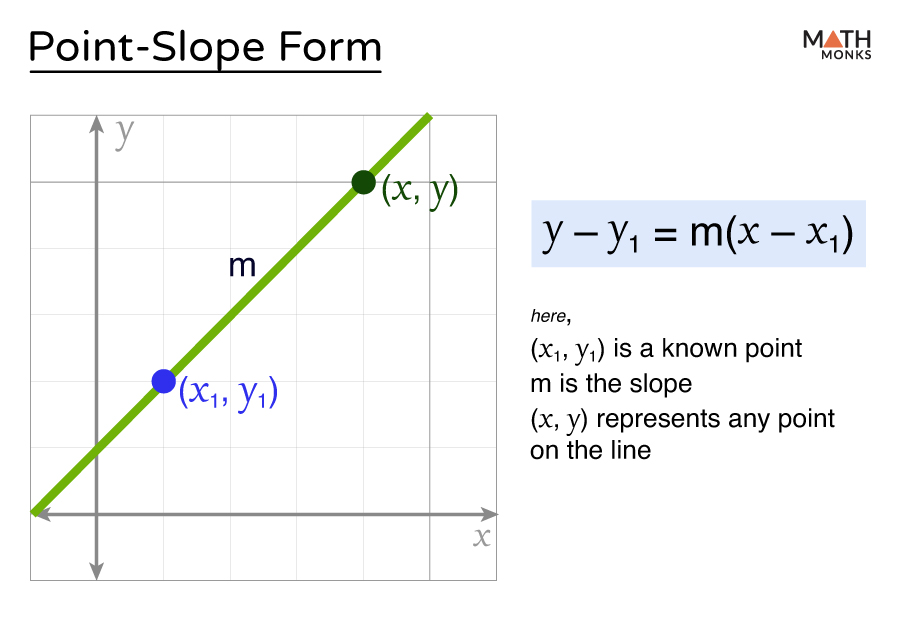
The point-slope form is one way of writing the equation of a straight line. It is particularly useful when we know a point on the line and its slope. The equation of a line in point-slope form is given by:
y – y1 = m(x – x1)
Here,
- (x1, y1) is a point on the line
- m is the slope
- (x, y) is a coordinate of any other point
An example of a linear equation in point-slope form is:
y – 3 = 4(x – 2)
Here, m = 4 and (x1, y1) = (3, 2)
The point-slope form is closely related to the slope-intercept form y = mx + b. Thus, by simplifying the point-slope form, we can derive the slope-intercept form of the equation.
This form is similar to the slope-intercept form. It is actually an extended slope-intercept form.
Derivation
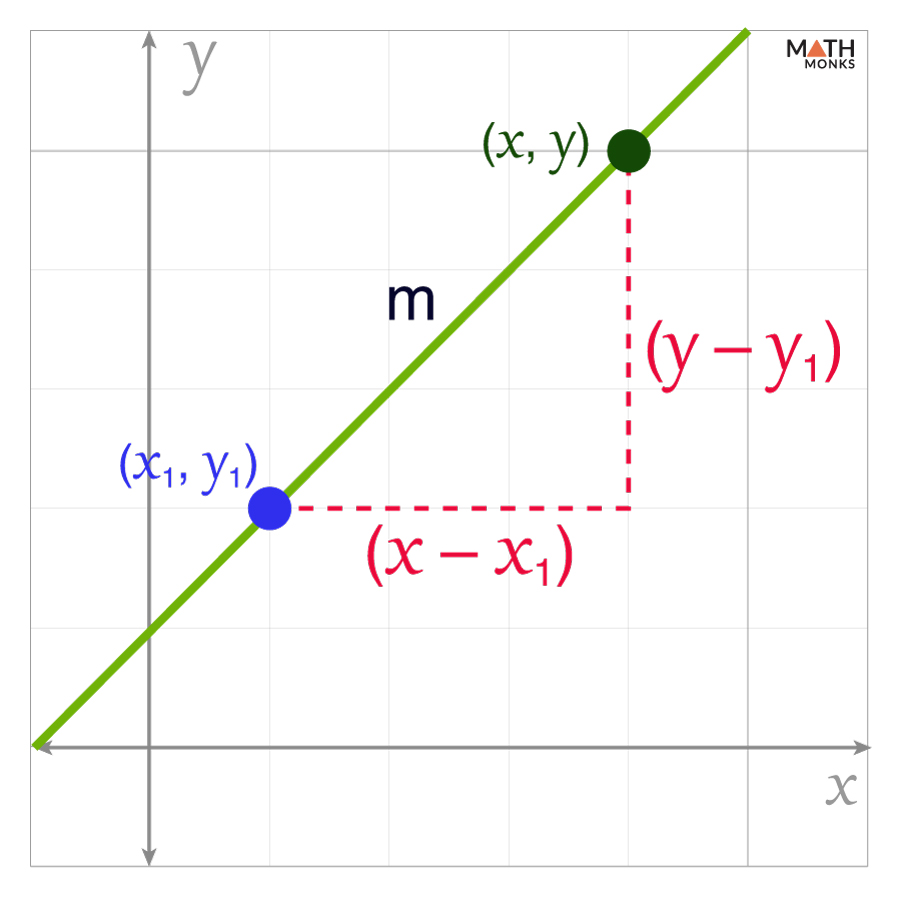
The formula is derived from the definition of the slope of a line:
m = ${\dfrac{change \ in \ y}{change \ in \ x}}$
Substituting the given point (x1, y1) and any point (x, y) on the line, we get:
⇒ m = ${\dfrac{y-y_{1}}{x-x_{1}}}$
Rearranging the equation by cross-multiplication, we obtain:
y – y1 = m(x – x1)
This is the point-slope form equation of a straight line.
Finding the Equation of a Line
Now, let us determine the equation of a line in point-slope form passing through (3, 2) with a slope of 4
As we know, the linear equation in point-slope form is:
y – y1 = m(x – x1)
Substituting the given values in the equation:
Thus, the equation is: y – 2 = 4(x – 3)
Rewriting Further:
Expanding the above equation and solving for y,
⇒ y – 2 = 4x – 12
⇒ y = 4x – 12 + 2
⇒ y = 4x – 10, which is the slope-intercept form of the linear equation.
⇒ y – 4x = -10
⇒ -4x + y = -10
⇒ 4x – y = 10, which is the standard form of the linear equation.
Graphing
When graphing a linear equation in point-slope form, we follow the following steps:
- Plotting the given point on the coordinate plane
- Using the slope to determine another point by moving vertically and horizontally
- Drawing the line through the two points
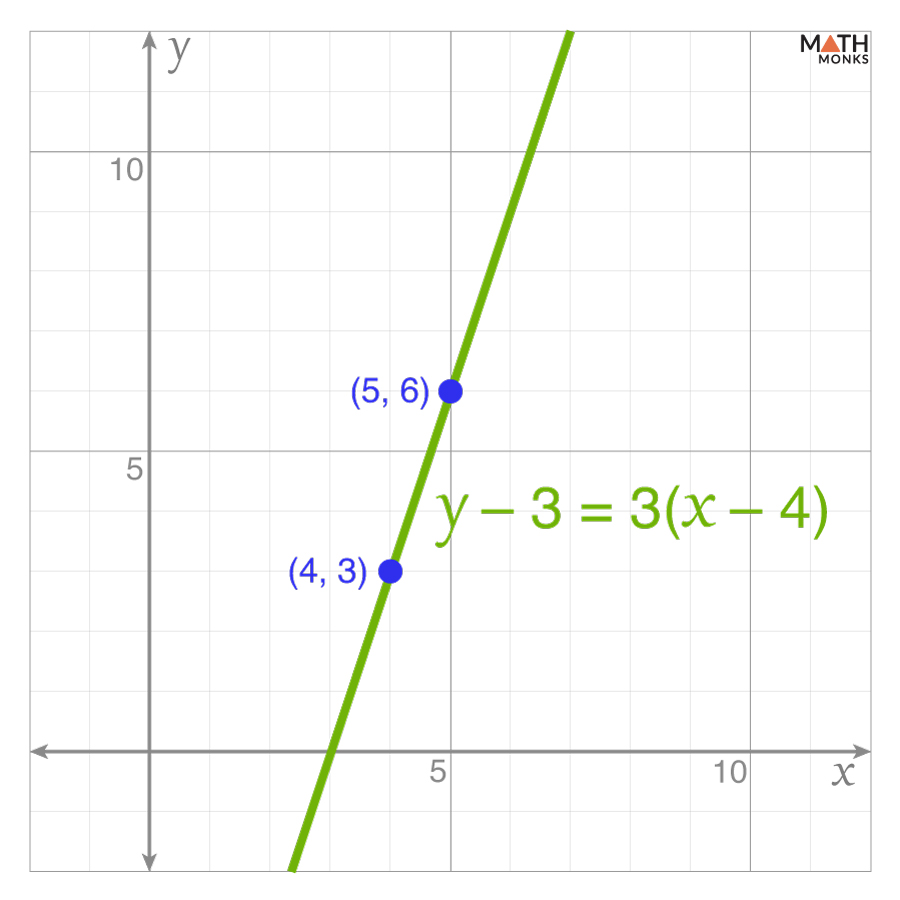
Let us plot y – 3 = 3(x – 4) on the coordinate plane.
Here,
The given point is (x1, y1) = (4, 3)
The slope is m = 3
Starting with the point (4, 3), we move 3 units up (positive rise) and 1 unit to the right (positive run), and we get another point as (5, 6)
Now, plotting the points (4, 3) and (5, 6), we get
Solved Examples
![]()
Write the equation of the line in the point-slope form that passes through the point (2, 5) with a slope of -3.
Solution:
![]()
As we know, the point-slope form of a line is y – y1 = m(x – x1)
Here,
The point is (x1, y1) = (2, 5)
The slope is m = -3
Thus, the equation of a line is: y – 5 = -3(x – 2)
![]()
Convert the equation ${y-4=\dfrac{3}{2}\left( x-6\right)}$ to slope-intercept form.
Solution:
![]()
Given, ${y-4=\dfrac{3}{2}\left( x-6\right)}$
⇒ ${y-4=\dfrac{3x}{2}-\dfrac{18}{2}}$
⇒ ${y-4=\dfrac{3x}{2}-9}$
⇒ ${y=\dfrac{3x}{2}-9+4}$
⇒ ${y=\dfrac{3x}{2}-5}$
Thus, the equation of the line in slope-intercept form is: ${y=\dfrac{3x}{2}-5}$
![]()
Convert ${y-2=-\dfrac{5}{3}\left( x-1\right)}$ to standard form.
Solution:
![]()
Given, ${y-2=-\dfrac{5}{3}\left( x-1\right)}$
⇒ ${y-2=-\dfrac{5x}{3}+\dfrac{5}{3}}$
⇒ ${y-2=\dfrac{-5x+5}{3}}$
⇒ 3(y – 2) = -5x + 5
⇒ 3y – 6 = -5x + 5
⇒ 3y + 5x = 5 + 6
⇒ 5x + 3y = 11
Thus, the equation of the line in standard form is 5x + 3y = 11
Problem: Writing equation in point-slope form when TWO POINTS are known
![]()
Find the equation of the line in the point-slope form passing through the points (3, 7) and (6, 13).
Solution:
![]()
As we know, the formula for the slope is:
m = ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$
Substituting (x1, y1) = (3, 7) and (x2, y2) = (6, 13),
m = ${\dfrac{13-7}{6-3}}$ = 2
Now, using the point (3, 7) and the slope 2,
y – y1 = m(x – x1)
⇒ y – 7 = 2(x – 3)
Thus, the equation of the line in the point-slope form is: y – 7 = 2(x – 3)
