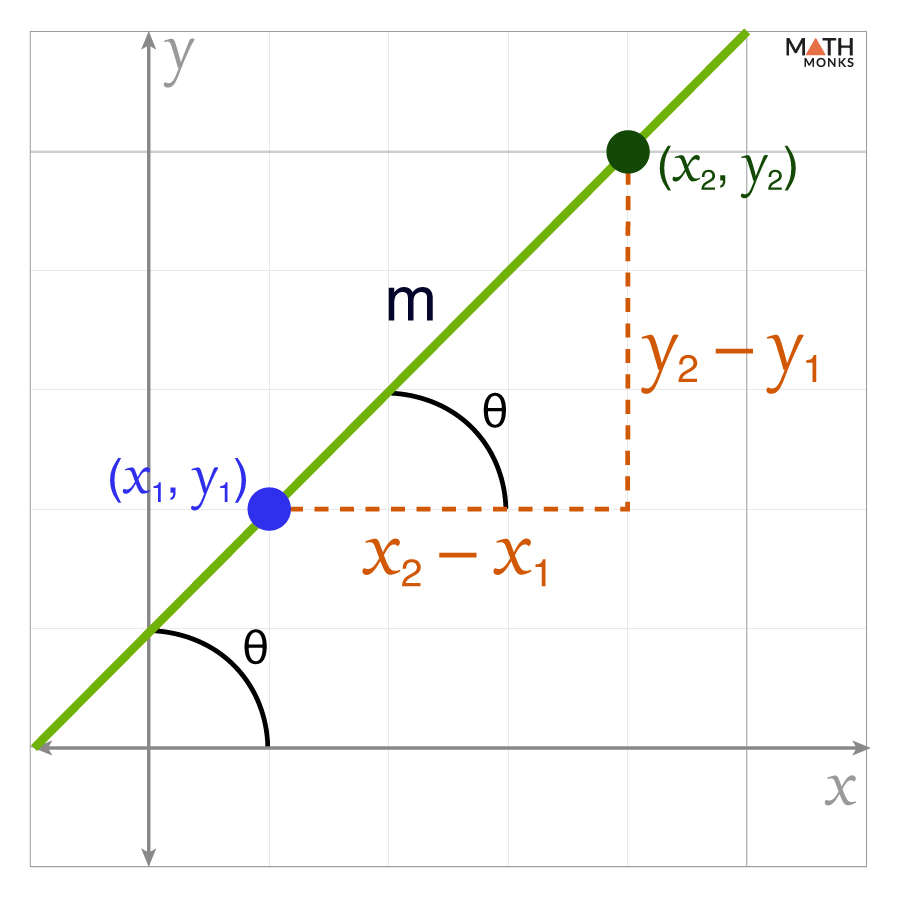
The slope of a line, denoted by m, is the rate of change between two points on a line and describes how much the line rises or falls as we move from left to right. It tells us how steep or flat the line is.
Formula
Mathematically,
Slope (m) = ${\dfrac{change \ in \ y}{change \ in \ x}}$
= ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$
Here,
- (x1, y1) and (x2, y2) are two points on the line
- (y2 – y1) is the vertical change (rise)
- (x2 – x1) is the horizontal change (run)
The slope of a line can also be represented by
m = tan θ = ${\dfrac{\Delta x}{\Delta y}}$
Rewriting the slope formula ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$, we will get the point-slope form of the equation y – y1 = m(x – x1)
Derivation
Let us consider a straight line passing through the points A(x1, y1) and B(x2, y2)
Finding the Change in Coordinates
- The vertical change (rise) is Δy = y2 – y1
- The horizontal change (run) is Δx = x2 – x1
Finding the Slope
Now, from the right-angled triangle ABC,
The slope is simply the tangent of the angle (θ) the line makes with the x-axis.
m = tan θ = ${\dfrac{opposite \ side}{adjacent \ side}}$
= ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$
Thus, the slope (m) = ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$
Types of Slope
The slope of a line can be:
Positive (m > 0)
The line rises from left to right. An uphill road has a positive slope.
Negative (m < 0)
The line falls from left to right. A downhill road has a negative slope.
Zero (m = 0)
It is a horizontal line. A flat road has zero slope.
Undefined
It is a vertical line. The slope of a wall or a tree trunk is undefined.
Finding the Slope
From Two Points
If we are given two points on a line, say (x1, y1) and (x2, y2), we can calculate the slope by using the slope formula:
m = ${\dfrac{change \ in \ y}{change \ in \ x}}$ = ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$
Let us consider two points (3, 5) and (7, 11)
To find the slope:
Calculating the change in y-coordinates,
y2 – y1 = 11 – 5 = 6
Calculating the change in x-coordinates,
x2 – x1 = 7 – 3 = 4
Now, finding the slope
m = ${\dfrac{change \ in \ y}{change \ in \ x}}$ = ${\dfrac{6}{4}}$ = ${\dfrac{3}{2}}$
Thus, the slope is: m = ${\dfrac{3}{2}}$
From an Equation
Sometimes, instead of two points, we are given the equation of a line. To determine the slope, we rewrite the equation in slope-intercept form:
y = mx + b …..(i)
For example, let us consider the equation: y = 4x – 7
By comparing it to the equation (i), we get
m = 4
Thus, the slope is m = 4.
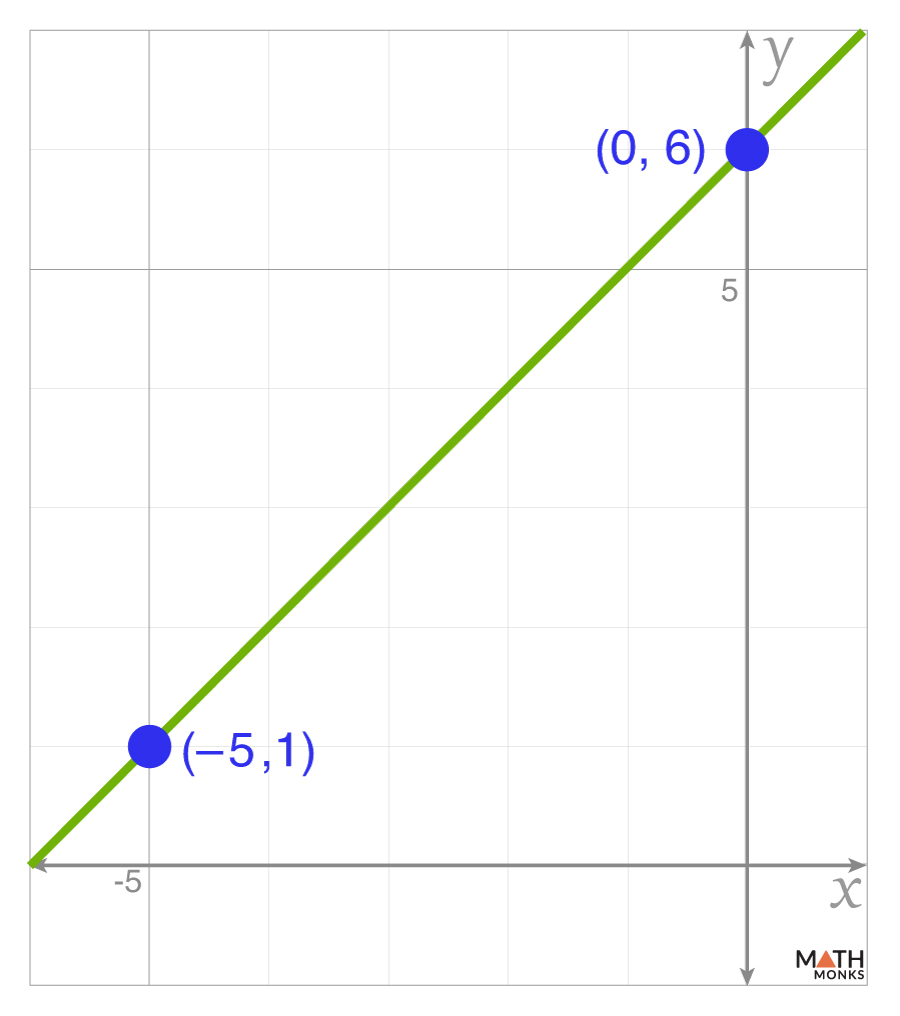
From a Graph
We can also calculate the slope from a graph by choosing any two points on the line and counting the rise (vertical change) and run (horizontal change).
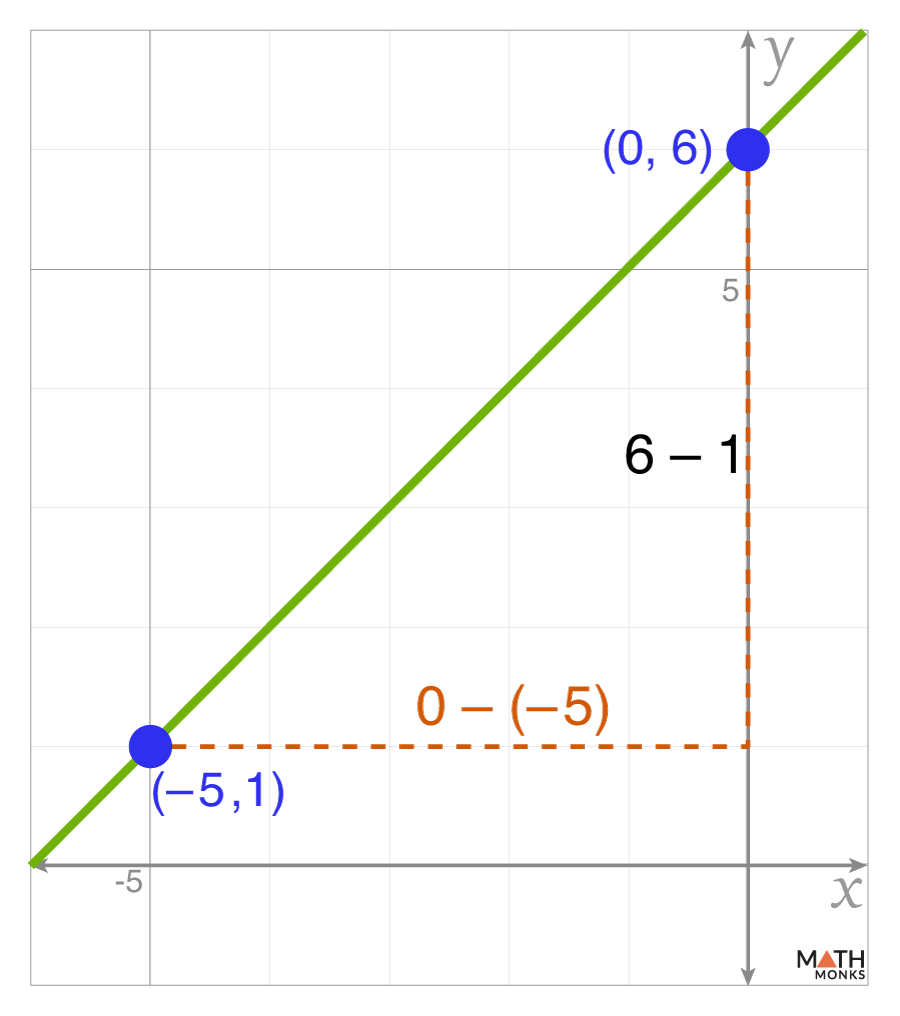
From the graph, we get the points (-5, 1) and (0, 6)
Now, calculating the rise
Rise = y2 – y1 = 6 – 1 = 5
Counting the number of units the line moves left (run), we get
Run = x2 – x1 = 0 – (-5) = 5
Applying the slope formula:
m = ${\dfrac{rise}{run}}$ = ${\dfrac{5}{5}}$ = 1
Thus, the slope is m = 1
Solved Examples
![]() Find the slope of the line passing through the points (4, 2) and (8, 10)
Find the slope of the line passing through the points (4, 2) and (8, 10)
Solution:
![]()
As we know, the slope formula is:
m = ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$
Here, (x1, y1) = (4, 2) and (x2, y2) = (8, 10)
Substituting the values,
m = ${\dfrac{10-2}{8-4}}$ = ${\dfrac{8}{4}}$ = 2
Thus, the slope is 2
![]() A line passes through the points (3, 5) and (k, 11). If the slope of the line is 2, find the value of k.
A line passes through the points (3, 5) and (k, 11). If the slope of the line is 2, find the value of k.
Solution:
![]()
As we know, the slope formula is:
m = ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$
Here, (x1, y1) = (3, 5), (x2, y2) = (k, 11), and m = 2
Substituting the values,
2 = ${\dfrac{11-5}{k-3}}$
⇒ 2(k – 3) = 11 – 5
⇒ 2k – 6 = 6
⇒ 2k = 6 + 6
⇒ 2k = 12
⇒ k = 6
Thus, the missing coordinate is k = 6
![]() Find the slope of the line given by the equation: 3x – 5y = 15
Find the slope of the line given by the equation: 3x – 5y = 15
Solution:
![]()
Given, 3x – 5y = 15
⇒ -5y = 15 – 3x
⇒ 5y = 3x – 15
⇒ y = ${\dfrac{3}{5}x-3}$
Comparing with y = mx + b, the slope is m = ${\dfrac{3}{5}}$
Thus, the slope is ${\dfrac{3}{5}}$