Last modified on March 26th, 2025

chapter outline

 

Parametric Equation of a Line

A parametric equation of a line represents a straight line by expressing its coordinates as functions of a variable, usually t. Instead of directly relating x and y, both (and z in 3D) are written in terms of t. 

This approach helps us to describe the position of a point on the line using a parameter, making it useful for understanding its direction and movement in the cartesian-coordinate plane.

Formulas

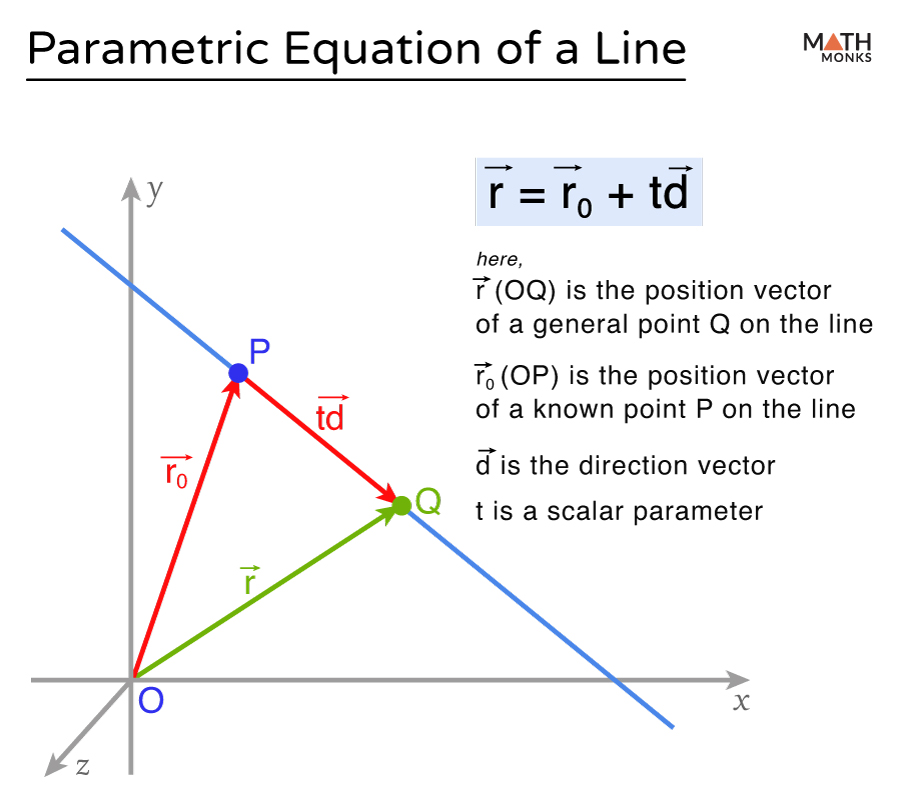
The vector equation of a line passing through a point P and parallel to a direction vector d is:

${\overrightarrow{r}=\overrightarrow{OP}+t\overrightarrow{d}}$

Parametric Equation of a Line

Here, P and d can be in either two or three dimensions.

In Two Dimensions (2D)

If a line passes through a point P(x₀, y₀) and has a direction vector d = (a, b), then its parametric equations are given by:

  • x = x0 + at
  • y = y0 + bt

Here,

  • t is the parameter
  • (x0, y0) is a known point on the line
  • (a, b) represents the direction of the line

Find the parametric equations of a line passing through the point (3, -2) with a direction vector (4, 5)

Solution:

Since both the point and the direction vector are in two dimensions, we determine the parametric equations of the line in this dimension.
As we know, the parametric equations in 2D are:
x = x0 + at
y = y0 + bt
Here, 
(x0, y0) = (3, -2) and (a, b) = (4, 5)
Substituting the values, we get
x = (3) + (4)t
y = (-2) + (5)t
Thus, the parametric equations of the line are:
x = 3 + 4t
y = -2 + 5t

In Three Dimensions (3D)

If a line passes through a point P(x0, y0, z0) and has a direction vector d = (a, b, c), its parametric equations are given by:

  • x = x0 + at
  • y = y0 + bt
  • z = z0 + ct

Here,

  • t is a parameter
  • (x0, y0, z0) is a known point on the line
  • (a, b, c) represents the direction of the line

Find the parametric equations of a line passing through the point (1, 2, 3) with a direction vector (-2, 4, 5)

Solution:

Since both the point and the direction vector are in three dimensions, we determine the parametric equations of the line in this dimension.
As we know, the parametric equations in 3D are:
x = x0 + at
y = y0 + bt
z = z0 + ct
Here,
(x0, y0, z0) = (1, 2, 3) and (a, b, c) = (-2, 4, 5)
Substituting the values, 
x = (1) + (-2)t
y = (2) + (4)t
z = (3) + (5)t
Thus, the parametric equations of the line are:
x = 1 – 2t
y = 2 + 4t
z = 3 + 5t

Problem: Finding the parametric equation of a line passing through TWO POINTS

Find the parametric equations of the line passing through the points A(1, 2, 3) and B(4, 6, 8).

Solution:

As we know, if two points (x0, y0, z0) and (x1, y1, z1) are given, the direction vector will be 
d = (x1 – x0, y1 – y0, z1 – z0)
Here, d = (4 – 1, 6 – 2, 8 – 3) = (3, 4, 5)
Now, by using the general parametric equation form,
x = x0 + (x1 – x0)t ⇒ x = 1 + 3t
y = y0 + (y1 – y0)t ⇒ y = 2 + 4t
z = z0 + (z1 – z0)t ⇒ z = 3 + 5t
​Here, t is a real number.
Thus, the parametric equations are: x = 1 + 3t, y = 2 + 4t, and z = 3 + 5t

Problem: Finding the parametric equation for the line of Intersection of TWO PLANES

Find the parametric equations of the line formed by the intersection of the planes:
2x – y + z = 5
x + y – 2z = 3

Solution:

Given, 
2x – y + z = 5 …..(i)
x + y – 2z = 3 …..(ii)
First, we solve for two variables in terms of the third. Let z = t, a parameter.
From equations (i) and (ii),
2x – y + t = 5 …..(iii)
x + y – 2t = 3 …..(iv)
Adding equations (iii) and (iv),
(2x – y + t) + (x + y – 2t) = 5 + 3
⇒ 2x + x – y + y + t – 2t = 8
⇒ 3x – t = 8
⇒ x = ${\dfrac{8+t}{3}}$
Substituting x into the equation (iv),
${\dfrac{8+t}{3}+y-2t=3}$
⇒ ${\dfrac{8+t+3y-6t}{3}=3}$
⇒ 8 + t + 3y – 6t = 9
⇒ 3y = 9 – 8 + 6t – t
⇒ 3y = 1 + 5t
⇒ y = ${\dfrac{1+5t}{3}}$
Thus, the parametric equations are: x = ${\dfrac{8+t}{3}}$, y = ${\dfrac{1+5t}{3}}$, and z = t

Converting to Symmetric Form

While parametric equations define a line using a parameter, they can also be rewritten in symmetric form to eliminate t and express the relationship between coordinates directly.

For a 3D line with parametric equations:

x = x0 + at

y = y0 + bt

z = z0 + ct

Now, solving for t in each equation, we get

t = ${\dfrac{x-x_{0}}{a}=\dfrac{y-y_{0}}{b}=\dfrac{z-z_{0}}{c}}$

This gives the symmetric form of the line:

${\dfrac{x-x_{0}}{a}=\dfrac{y-y_{0}}{b}=\dfrac{z-z_{0}}{c}}$

Now, let us convert the following parametric equations to the symmetric form:

x = 2 + 3t …..(i)

y = 5 + 4t …..(ii)

Now, solving for t, we get

x = 2 + 3t ⇒ 3t = x – 2 ⇒ t = ${\dfrac{x-2}{3}}$

y = 5 + 4t ⇒ 4t = y – 5 ⇒ t = ${\dfrac{y-5}{4}}$

Thus, the symmetric form of the line is:

${\dfrac{x-2}{3}=\dfrac{y-5}{4}}$

Convert the following parametric equations of a line in 3D in the symmetric form:
x = 1 – 2t
y = 2 + 4t
z = 3 + 5t

Solution:

Given, 
x = 1 – 2t …..(i)
y = 2 + 4t …..(ii)
z = 3 + 5t …..(iii)
Using (i),
x = 1 – 2t
⇒ 2t = 1 – x
⇒ 2t = -(x – 1)
⇒ t = ${-\dfrac{x-1}{2}}$ …..(iv)
Using (ii),
y = 2 + 4t
⇒ 4t = y – 2
⇒ t = ${\dfrac{y-2}{4}}$ …..(v)
Using (iii),
z = 3 + 5t
⇒ 5t = z – 3
⇒ t = ${\dfrac{z-3}{5}}$ …..(vi)
From (iv), (v), and (vi), the symmetric equations are:
${-\dfrac{x-1}{2}=\dfrac{y-2}{4}=\dfrac{z-3}{5}}$

Last modified on March 26th, 2025