The Gamma Function is a function that extends the concept of factorials beyond whole numbers. As we know, the formula of the factorials is:
n! = n × (n – 1) × (n – 2) × ⋯ × 2 × 1
It works well for whole numbers like 1, 2, and 3. However, to find ${\left( \dfrac{1}{2}\right) !}$ or (-3.5)!, we need the Gamma Function. The Gamma Function is represented by the symbol Γ(n) (read as ‘gamma of n’).
Thus, it is a generalized version of the factorial function that works for all real and complex numbers except non-positive integers.
Mathematically, it is defined as:
${\Gamma \left( z\right) =\int ^{\infty }_{0}x^{z-1}e^{-x}dx}$
The Gamma Function is used in probability and statistics like gamma and chi-square distributions, as well as in complex analysis, including Bessel and Legendre functions.
Properties
Recurrence Relation
Just like n! = n × (n-1)!, the gamma function satisfies the recurrence relation:
Γ(z+1) = z Γ(z), which allows us to calculate values step by step.
For example,
Γ(3.5) = 2.5 Γ(2.5) = 2.5 × 1.5 Γ(1.5)
This makes calculations easier without directly integrating the function.
Value at Half-Integer Points
The Gamma function has a well-known value at half-integer points:
${\Gamma \left( \dfrac{1}{2}\right) =\sqrt{\pi }}$
This result is essential in probability and statistics, particularly in the normal distribution and beta function.
Reflection Formula
This formula helps find gamma function values for negative inputs:
${\Gamma \left( z\right) \Gamma \left( 1-z\right) =\dfrac{\pi }{\sin \left( \pi z\right) }}$
Behavior for Negative Values
The Gamma Function is not defined for negative integers (e.g., Γ(-1), Γ(-2), Γ(-3), …) because it has poles at these points (tends to infinity). However, for negative non-integer values, the function is well-defined and can be computed using the reflection formula.
This formula allows us to compute Gamma values for negative non-integers using their positive counterparts.
For example,
${\Gamma \left( -\dfrac{1}{2}\right) \Gamma \left( 1+\dfrac{1}{2}\right) =\dfrac{\pi }{\sin \left( \pi \left( -\dfrac{1}{2}\right) \right) }}$
⇒ ${\Gamma \left( -\dfrac{1}{2}\right) =\dfrac{\pi }{\sin \left( -\dfrac{\pi }{2}\right) \times \Gamma \left( \dfrac{3}{2}\right) }}$
⇒ ${\Gamma \left( -\dfrac{1}{2}\right) =\dfrac{\pi }{-1\times \dfrac{\sqrt{\pi }}{2}}}$
⇒ ${\Gamma \left( -\dfrac{1}{2}\right) =-\dfrac{2\sqrt{\pi }}{\sqrt{\pi }}}$
⇒ ${\Gamma \left( -\dfrac{1}{2}\right) =-2}$
Evaluating Gamma Function
Let us evaluate the value of Γ(5) using the recurrence relation:
As we know, Γ(n) = (n – 1)!
Here, Γ(5) = (5 – 1)! = 4! = 4 × 3 × 2 × 1 = 24
Thus, Γ(5) = 24
For Fractions
For fractional values, the gamma function formula becomes:
${\Gamma \left( \dfrac{1}{2}\right) =\sqrt{\pi }}$
By using the recurrence relation: ${\Gamma \left( z+1\right) =z\Gamma \left( z\right)}$
We can determine values for other fractions as well.
For example,
${\Gamma \left( \dfrac{3}{2}\right) =\dfrac{1}{2}\Gamma \left( \dfrac{1}{2}\right) =\dfrac{\sqrt{\pi }}{2}}$
${\Gamma \left( \dfrac{5}{2}\right) =\dfrac{3}{2}\Gamma \left( \dfrac{3}{2}\right) =\dfrac{3}{2}\times \dfrac{\sqrt{\pi }}{2}=\dfrac{3\sqrt{\pi }}{4}}$
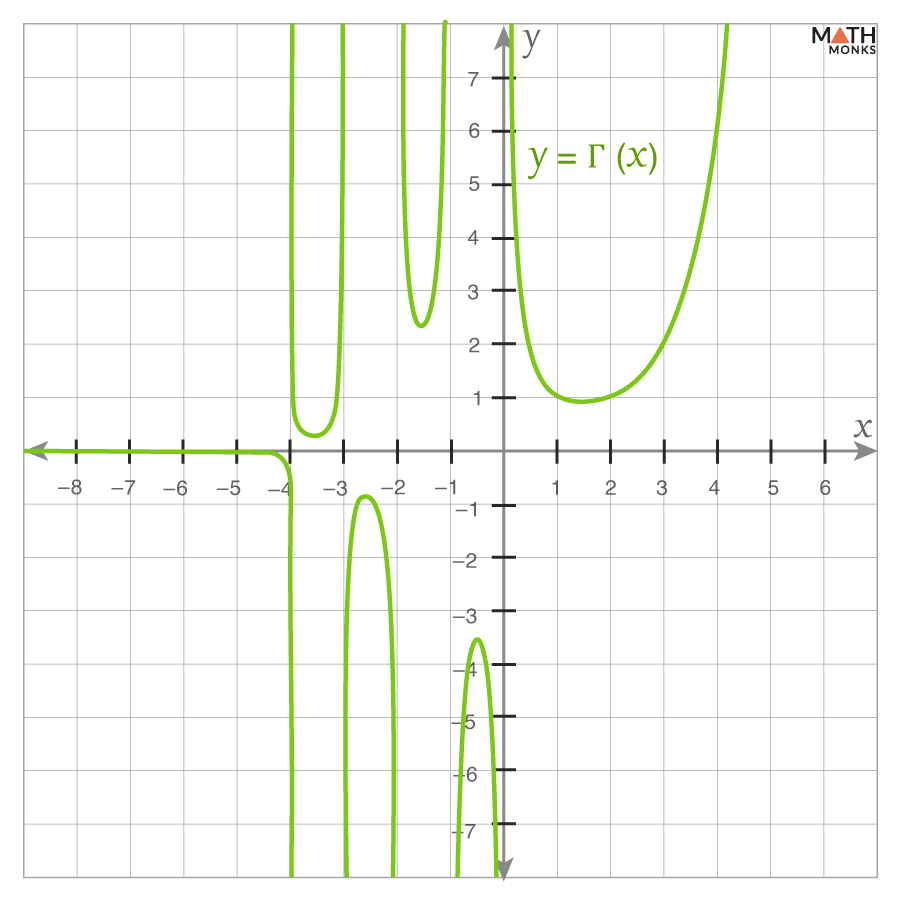
By Graphing
As we know, the Gamma Function extends the concept of factorials to non-integer and complex numbers. For positive integers, it follows the familiar pattern Γ(n) = (n – 1)!, but for non-integer values, it smoothly interpolates between these points.
However, at negative integers, it is undefined and diverges to infinity.
The graph below visually represents these key properties:
- For positive integers, Γ(x) follows factorial values.
- For fractional values, Γ(x) smoothly varies without abrupt jumps.
- At negative integers, vertical asymptotes (green dashed lines) indicate poles where Γ(x) is undefined.
This visualization highlights how the Gamma Function generalizes factorials while also showing its limitations at negative integers.
Note: The Gamma Function also applies to complex numbers, provided that their real part is greater than zero.
Solved Examples
![]() Find the value of ${\Gamma \left( \dfrac{3}{2}\right)}$
Find the value of ${\Gamma \left( \dfrac{3}{2}\right)}$
Solution:
![]()
As we know, Γ(z + 1) = z Γ(z)
Here,
${\Gamma \left( \dfrac{3}{2}\right) =\dfrac{1}{2}\Gamma \left( \dfrac{1}{2}\right)}$
Since ${\Gamma \left( \dfrac{1}{2}\right) =\sqrt{\pi }}$
Thus, ${\Gamma \left( \dfrac{3}{2}\right) =\dfrac{\sqrt{\pi }}{2}}$
![]() Use the recurrence relation to find Γ(4.5) given that Γ(0.5) = ${\sqrt{\pi }}$
Use the recurrence relation to find Γ(4.5) given that Γ(0.5) = ${\sqrt{\pi }}$
Solution:
![]()
As we know, Γ(z + 1) = z Γ(z)
Here,
Γ(4.5) = 3.5 Γ(3.5)
Γ(3.5) = 2.5 Γ(2.5)
Γ(2.5) = 1.5 Γ(1.5)
Given, Γ(0.5) = ${\sqrt{\pi }}$
Using Γ(1.5) = ${\dfrac{1}{2}\Gamma \left( 0.5\right) =\dfrac{\sqrt{\pi }}{2}}$, we get
${\Gamma \left( 2.5\right) =1.5\times \dfrac{\sqrt{\pi }}{2}=\dfrac{3\sqrt{\pi }}{4}}$
${\Gamma \left( 3.5\right) =2.5\times \dfrac{3\sqrt{\pi }}{4}=\dfrac{15\sqrt{\pi }}{8}}$
${\Gamma \left( 4.5\right) =3.5\times \dfrac{15\sqrt{\pi }}{8}=\dfrac{52.5\sqrt{\pi }}{16}}$
Thus, Γ(4.5) = ${\dfrac{52.5\sqrt{\pi }}{16}}$
Incomplete Gamma Function
The incomplete gamma function is a generalized form of the gamma function that we use to evaluate the function over a partial range of integration. Unlike the complete Gamma function, which integrates from 0 to ∞, the incomplete Gamma function integrates the value over a limited range.
Types
1. Lower Incomplete Gamma Function:
${\gamma \left( s,x\right) =\int ^{x}_{0}t^{s-1}e^{-t}dt}$
It integrates from 0 to x and is used in cumulative probability calculations.
2. Upper Incomplete Gamma Function:
${\Gamma \left( s,x\right) =\int ^{\infty }_{x}t^{s-1}e^{-t}dt}$
It integrates from x to ∞ and is used in tail probabilities and special functions.
Relation to the Complete Gamma Function
The incomplete gamma functions relate to the complete gamma function:
${\Gamma \left( s\right) =\gamma \left( s,x\right) +\Gamma \left( s,x\right)}$
This means that the sum of the lower and upper incomplete gamma functions gives the complete Gamma function.