Slope-Intercept Form

The slope-intercept form is one of the most common ways of representing a straight line. It is used when we need to find the linear equation given the slope and the y-intercept.

Formula

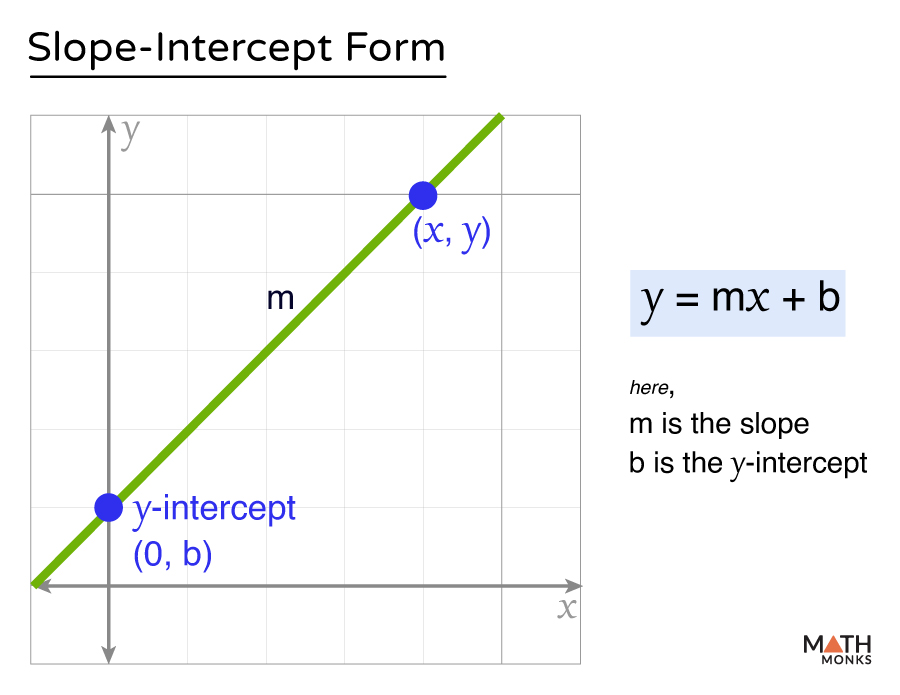
The slope-intercept form is given by:

y = mx + b

Here,

• m is the slope of the line
• b is the y-intercept.

An example of a linear equation in the slope-intercept form is:

y = 4x – 1

Here, m = 4, and the y-intercept is at (0, -1)

Slope

The slope (m) represents the steepness of a line. It is measured by the change in y for every unit increase in x. 

Mathematically, 

Slope (m) = ${\dfrac{change \  in \  y}{change \  in \  x}}$

 = ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$

 Here,

(x₁, y₁) and (x₂, y₂) are two points on the line

Y-Intercept

The y-intercept (b) is the point where the line touches or crosses the y-axis. It is the value that y takes when x = 0

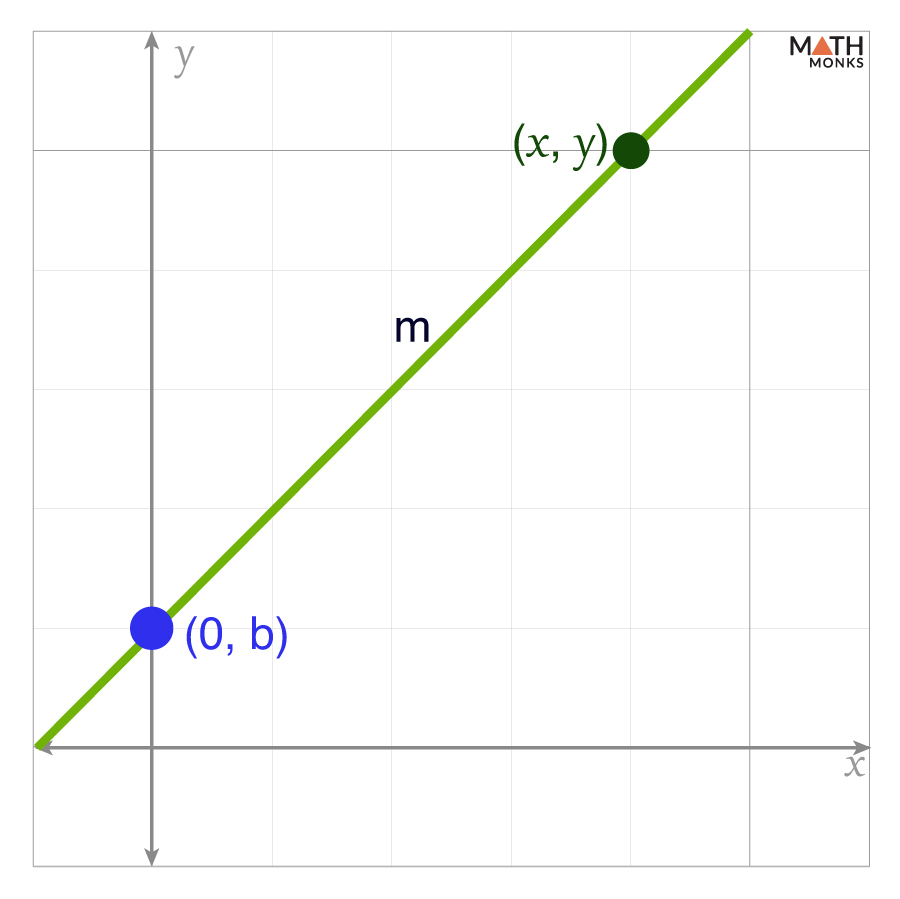
Derivation

Let us consider a straight line with a slope m that intersects the y-axis at the point (0, b), where b is the y-intercept. Let (x, y) be an arbitrary point on the same line.

As we know, the slope (m) of a line is given by:

m = ${\dfrac{change \  in \  y}{change \  in \  x}}$ = ${\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}}$

Here, (x₁, y₁) = (0, b) and (x₂, y₂) = (x, y)

Now, by calculating m, we get

m = ${\dfrac{y-b}{x-0}}$

⇒ m = ${\dfrac{y-b}{x}}$

⇒ mx = y – b

⇒ y = mx + b, which is the slope-intercept form of a straight line

Finding the Equation of a Line

Now, let us determine the equation of a line passing through the points (2, 5) and (4, 9)

As we know, the slope-intercept form is y = mx + c

Here,

The slope is m = ${\dfrac{9-5}{4-2}=\dfrac{4}{2}=2}$

Now, to find the y-intercept, we use the point (2, 5)

y = mx + b

⇒ 5 = 2(2) + b (since m = 2)

⇒ 5 = 4 + b

⇒ b = 5 – 4

⇒ b = 1

Thus, the y-intercept is (0, 1), and the equation is y = 2x + 1

Graphing

For graphing a linear equation in slope-intercept form, we follow the following points:

1. Plotting the y-intercept (b) on the y-axis
2. Using the slope (m) to find another point
3. Drawing a straight line through the points 

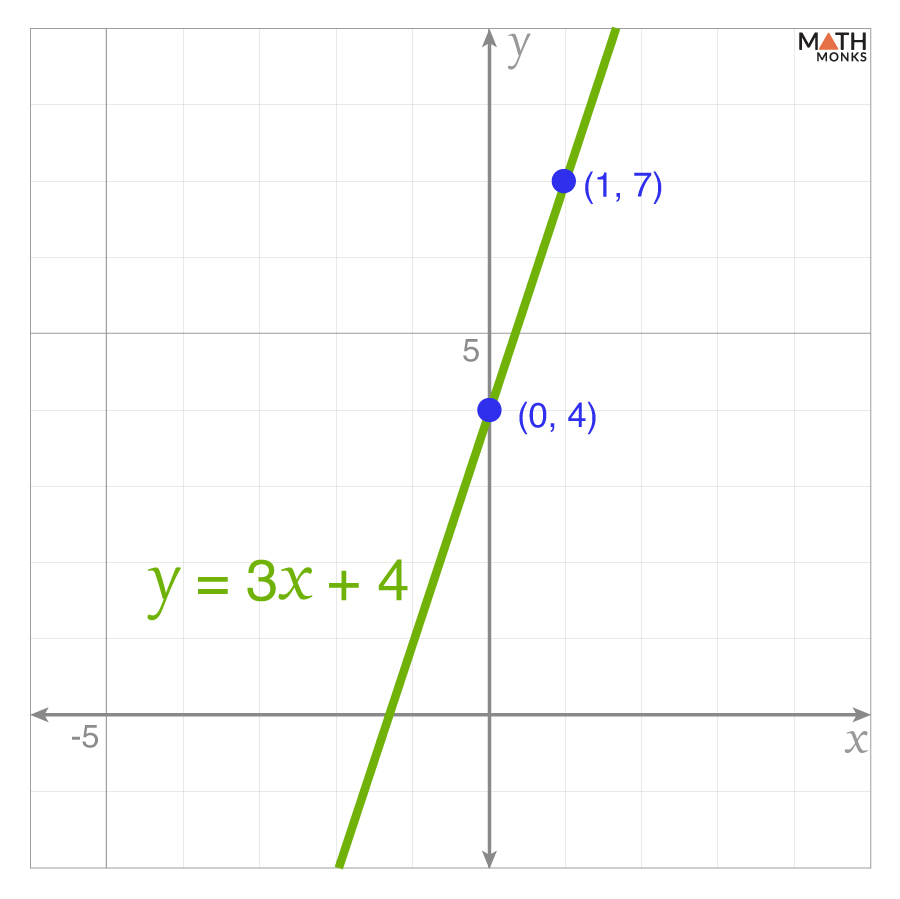
Let us plot y = 3x + 4 on the coordinate plane.

Here, 

The y-intercept is 4

Thus, the coordinates of the y-intercept are (0, 4)

Now, to find another point, we use the slope m = 3

Starting with the point (0, 4), we move 3 units up (positive rise) and 1 unit to the right (positive run), and we get another point as (1, 7)

Now, plotting the points (0, 4) and (1, 7), we get

Note: If m = 0, the line is horizontal. For example, y = 4.

Solved Examples