An improper fraction is a fraction in which the numerator is greater than or equal to the denominator. Thus, the value of an improper fraction is always greater than or equal to 1.
${\dfrac{3}{2}}$, ${\dfrac{8}{5}}$, ${\dfrac{28}{11}}$, ${\dfrac{7}{3}}$, ${\dfrac{13}{4}}$, and ${\dfrac{48}{15}}$ are a few improper fractions
Visualizing
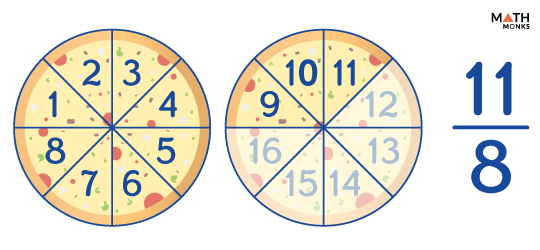
Let us suppose that several pizzas are ordered for a house party, and each pizza is cut into 8 slices.
Now, let’s say one of your friends has 11 slices of pizza. Since each pizza has 8 slices, he had more than one whole pizza. This can be represented as ${\dfrac{11}{8}}$, which is an improper fraction.
The above situation is represented in the diagram below:
Improper Fractions to Mixed Numbers
Sometimes, we need to represent an improper fraction as a mixed number. To convert, we first divide the numerator of the given fraction by the denominator and then convert it into a mixed fraction.
Let us convert the fraction ${\dfrac{11}{8}}$ to its corresponding mixed number using our pizza example.
By dividing 11 by 8, we get the quotient as 1, representing a whole pizza, and the remainder of 3 means there are 3 extra slices (the fractional part).
Representing the remainder as fraction, we get ${\dfrac{3}{8}}$
Now, combining the whole and the fractional part, we get the improper fraction as ${\dfrac{11}{8}}$.
Now, dividing the numerator (11) by the denominator (8), we get the mixed fraction ${1\dfrac{3}{8}}$
Improper Fraction to Decimals
To convert an improper fraction to a decimal number, we simply divide the numerator by the denominator of the given fraction.
Dividing the improper fraction ${\dfrac{11}{8}}$, we get
11 ÷ 8 = 1.375
On a Number Line
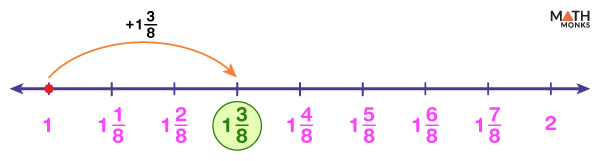
Let us now represent the same improper fraction ${\dfrac{11}{8}}$ on a number line.
1. Drawing the Number Line
We start by drawing a number line and marking each interval by the corresponding whole numbers (0, 1, 2, 3…)
2. Converting the Improper Fraction into a Mixed Number
${\dfrac{11}{8}}$ = ${1\dfrac{3}{8}}$
3. Marking the Whole Numbers on the Number Line
Since the whole number is 1, we mark 1 and 2 on the number line as ${1\dfrac{3}{8}}$ lies between 1 and 2.
4. Dividing the Number Line into Intervals
The region between 1 and 2 is divided into 8 equal parts (as the denominator is 8), and each part is marked as ${\dfrac{1}{8}}$, ${\dfrac{2}{8}}$, and so on.
5. Locating the Mixed Number
Now, the third interval from 1 is marked as ${1\dfrac{3}{8}}$
Simplifying
To simplify, an improper fraction means to express the fraction in its lowest term. Thus, we divide the numerator and denominator by their greatest common factor (GCF).
Let us simplify the improper fraction ${\dfrac{28}{20}}$
Factorizing the numerator and the denominator, we get
28 = 2 × 2 × 7
20 = 2 × 2 × 5
Thus, the GCF of 28 and 20 is 4
Now, by dividing the numerator and the denominator by 4, we get
${\dfrac{28}{20}}$
= ${\dfrac{7}{5}}$
Adding
When adding improper fractions, we can have two cases:
With the Same Denominators
To add improper fractions with the same denominator, we follow the following steps:
Let us add ${\dfrac{7}{4}}$ and ${\dfrac{11}{4}}$
Step 1: Adding the numerators together
${\dfrac{7}{4}+\dfrac{11}{4}}$
= ${\dfrac{7+11}{4}}$
Step 2: Simplifying
= ${\dfrac{18}{4}}$
= ${\dfrac{9}{2}}$
With Different Denominators
Let us add ${\dfrac{7}{2}+\dfrac{9}{4}}$
Step 1: Finding the LCM of the denominators
Here, the denominators are 2 and 4
The LCM of 2 and 4 is 4
Step 2: Rationalizing the denominators
Now, to rationalize, we will multiply the first fraction by 2 and the second fraction by 1
${\dfrac{7\times 2}{2\times 2}+\dfrac{9\times 1}{4\times 1}}$
= ${\dfrac{14}{4}+\dfrac{9}{4}}$.
Step 3: Adding the numerators together
= ${\dfrac{14+9}{4}}$
Step 4: Simplifying
= ${\dfrac{23}{4}}$
Subtracting
Subtraction of improper fractions is similar to addition.
With the Same Denominators
If we subtract ${\dfrac{4}{3}}$ from ${\dfrac{14}{3}}$
${\dfrac{14}{3}-\dfrac{4}{3}}$
= ${\dfrac{14-4}{3}}$
= ${\dfrac{10}{3}}$
With Different Denominators
If we subtract ${\dfrac{4}{3}}$ from ${\dfrac{9}{5}}$
${\dfrac{9}{5}-\dfrac{4}{3}}$
= ${\dfrac{9\times 3}{5\times 3}-\dfrac{4\times 5}{3\times 5}}$
= ${\dfrac{27}{15}-\dfrac{20}{15}}$
= ${\dfrac{27-20}{15}}$
= ${\dfrac{7}{15}}$
Multiplying
While multiplying improper fractions, we multiply the numerators and the denominators separately.
Let us multiply ${\dfrac{7}{3}}$ and ${\dfrac{11}{5}}$
${\dfrac{7}{3}\times \dfrac{11}{5}}$
= ${\dfrac{7\times 11}{3\times 5}}$
= ${\dfrac{77}{15}}$
Dividing
While dividing, we multiply the first fraction by the reciprocal of the second fraction.
Let us divide ${\dfrac{7}{2}}$ by ${\dfrac{11}{5}}$
${\dfrac{7}{2}\div \dfrac{11}{5}}$
= ${\dfrac{7}{2}\times \dfrac{5}{11}}$
= ${\dfrac{7\times 5}{2\times 11}}$
= ${\dfrac{35}{22}}$
Solved Examples
![]() Write ${2\dfrac{1}{3}}$ as an improper fraction.
Write ${2\dfrac{1}{3}}$ as an improper fraction.
Solution:
![]()
Here,
The denominator = 3
The numerator = 1
The whole number = 2
Now, by multiplying 2 by 3 and then adding 1 to it, we get
(2 × 3) + 1 = 7
Thus, ${2\dfrac{1}{3}}$ = ${\dfrac{7}{3}}$
![]() Identify the improper fractions:
Identify the improper fractions:
${\dfrac{5}{3}}$, ${\dfrac{7}{9}}$, ${\dfrac{37}{13}}$, ${\dfrac{25}{12}}$, ${\dfrac{9}{43}}$, and ${\dfrac{2}{3}}$
Solution:
![]()
Here, the improper fractions are: ${\dfrac{5}{3}}$, ${\dfrac{37}{13}}$, and ${\dfrac{25}{12}}$