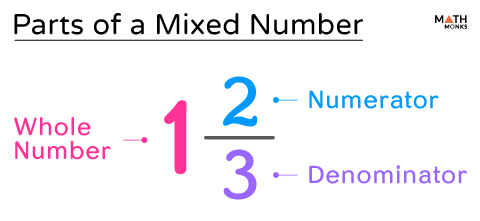A mixed number, also called a mixed fraction, consists of a whole number and a proper fraction. Mixed numbers represent quantities that are more than one whole but less than the next whole number.
${1\dfrac{2}{3}}$, ${1\dfrac{2}{5}}$, ${4\dfrac{5}{7}}$, ${2\dfrac{1}{6}}$, and ${1\dfrac{3}{4}}$ are a few examples of mixed number.
Parts
It has two main parts: the whole number and the fractional part. The fractional part again consists of a numerator and a denominator.
- Whole number
- Fractional part
- Numerator
- Denominator
Here are a few more real-life examples of mixed numbers:
- When serving a cake or a pie at home, we express the parts of a whole as mixed fractions.
- A piece of wood of ${3\dfrac{3}{7}feet}$ long is expressed in mixed fraction
- A fully filled glass of milk and a half-filled glass is represented in mixed fraction as ${1\dfrac{1}{2}}$.
Mixed Numbers to Improper Fractions
To convert a mixed number to an improper fraction, we first multiply the denominator with the whole number, then add the resultant product with the numerator.
Let us convert ${1\dfrac{2}{5}}$ to improper fraction.
Here, we will multiply the denominator 5 by the whole number 1
1 × 5 = 5
Now, on adding the numerator of the mixed number 2 to the result 5,
2 + 5 = 7
Keeping the denominator the same and placing the sum in the numerator, we get the improper fraction
${\dfrac{7}{5}}$
Mixed Numbers to Decimals
Method 1
To convert a mixed number to a decimal, we change the number to an improper fraction and then divide the numerator by the denominator.
Let us convert ${1\dfrac{3}{8}}$ to decimal number.
Here, converting ${1\dfrac{3}{8}}$ into improper fraction, we get
${\dfrac{\left( 1\times 8\right) +3}{8}}$ = ${\dfrac{11}{8}}$
Now, by dividing the numerator 11 by the denominator 8, we get
11 ÷ 8 = 1.375
Method 2
To convert a mixed number to a decimal, we convert the fractional part to a decimal and then add the result to the whole number part.
Again, we convert ${1\dfrac{3}{8}}$ to decimal number.
Here, the fractional part is ${\dfrac{3}{8}}$
On dividing the numerator 3 by the denominator 8, we get
3 ÷ 8 = 0.375
Now, on adding the result to the whole number part 1, we get
1 + 0.375 = 1.375
Adding
To add mixed numbers, we first convert them into improper fractions and simplify them.
Let us add ${4\dfrac{5}{7}+1\dfrac{2}{3}}$
First, converting the mixed numbers ${4\dfrac{5}{7}}$ and ${1\dfrac{2}{3}}$ to improper fractions, we get
${4\dfrac{5}{7}}$ = ${\dfrac{\left( 4\times 7\right) +5}{7}}$ = ${\dfrac{33}{7}}$
${1\dfrac{2}{3}}$ = ${\dfrac{\left( 1\times 3\right) +2}{3}}$ = ${\dfrac{5}{3}}$
Now, if the denominators are the same, we add the numerators. However, if they are different, we take the LCM of the denominators and then simplify
Here, the denominators are 7 and 3, that are different.
The LCM of 7 and 3 is 21
Now, ${\dfrac{33}{7}+\dfrac{5}{3}}$
= ${\dfrac{33\times 3}{7\times 3}+\dfrac{5\times 7}{3\times 7}}$
= ${\dfrac{99}{21}+\dfrac{35}{21}}$
= ${\dfrac{99+35}{21}}$
= ${\dfrac{134}{21}}$
= ${6\dfrac{8}{21}}$
Subtracting
To subtract, we follow the same steps as addition.
Converting the mixed numbers ${4\dfrac{5}{7}}$ and ${1\dfrac{2}{3}}$ to improper fractions, we get
${4\dfrac{5}{7}}$ = ${\dfrac{\left( 4\times 7\right) +5}{7}}$ = ${\dfrac{33}{7}}$
${1\dfrac{2}{3}}$ = ${\dfrac{\left( 1\times 3\right) +2}{3}}$ = ${\dfrac{5}{3}}$
Here, the denominators are 7 and 3, that are different.
The LCM of 7 and 3 is 21
${4\dfrac{5}{7}-1\dfrac{2}{3}}$
= ${\dfrac{\left( 4\times 7\right) +5}{7}-\dfrac{\left( 1\times 3\right) +2}{3}}$
= ${\dfrac{33}{7}-\dfrac{5}{3}}$
= ${\dfrac{33\times 3}{7\times 3}-\dfrac{5\times 7}{3\times 7}}$
= ${\dfrac{99}{21}-\dfrac{35}{21}}$
= ${\dfrac{99-35}{21}}$
= ${\dfrac{64}{21}}$
= ${3\dfrac{1}{21}}$
Multiplying
To multiply improper fractions, we first convert the mixed numbers to improper fractions and then multiply the numerators and denominators separately.
Let us multiply ${3\dfrac{2}{5}}$ and ${2\dfrac{7}{8}}$
Converting the mixed numbers ${3\dfrac{2}{5}}$ and ${2\dfrac{7}{8}}$ to improper fractions, we get:
${3\dfrac{2}{5}}$ = ${\dfrac{\left( 3\times 5\right) +2}{5}}$ = ${\dfrac{17}{5}}$
${2\dfrac{7}{8}}$ = ${\dfrac{\left( 2\times 8\right) +7}{8}}$ = ${\dfrac{23}{8}}$
Now, multiplying the numerators and the denominators separately, we get
${\dfrac{17}{5}\times \dfrac{23}{8}}$
= ${\dfrac{17\times 23}{5\times 8}}$
= ${\dfrac{391}{40}}$
= ${9\dfrac{31}{40}}$
Dividing
Dividing mixed fractions is easy. First, we convert the mixed numbers to improper fractions and then multiply the first fraction by the reciprocal of the second fraction.
Let us divide ${3\dfrac{2}{5}}$ by ${2\dfrac{7}{8}}$
Converting the mixed numbers ${3\dfrac{2}{5}}$ and ${2\dfrac{7}{8}}$ to improper fractions,we get:
${3\dfrac{2}{5}}$ = ${\dfrac{\left( 3\times 5\right) +2}{5}}$ = ${\dfrac{17}{5}}$
${2\dfrac{7}{8}}$ = ${\dfrac{\left( 2\times 8\right) +7}{8}}$ = ${\dfrac{23}{8}}$
Then, multiplying the first fraction by the reciprocal of the second fraction
${\dfrac{17}{5}\times \dfrac{8}{23}}$
= ${\dfrac{17\times 8}{5\times 23}}$
= ${\dfrac{136}{115}}$
Solved Examples
![]() Convert the fraction ${\dfrac{13}{12}}$ into a mixed number.
Convert the fraction ${\dfrac{13}{12}}$ into a mixed number.
Solution:
![]()
Given ${\dfrac{13}{12}}$
On dividing the numerator 13 by the denominator 12, we get
13 ÷ 12
The quotient is 1
The remainder is 1
As we know,
${Quotient\dfrac{Remainder}{Divisor}}$
Thus, ${\dfrac{13}{12}}$ = ${1\dfrac{1}{12}}$
![]() Add the mixed numbers ${2\dfrac{3}{5}}$ and ${1\dfrac{4}{9}}$
Add the mixed numbers ${2\dfrac{3}{5}}$ and ${1\dfrac{4}{9}}$
Solution:
![]()
Here, ${2\dfrac{3}{5}+1\dfrac{4}{9}}$
= ${\dfrac{\left( 2\times 5\right) +3}{5}+\dfrac{\left( 1\times 9\right) +4}{9}}$
= ${\dfrac{13}{5}+\dfrac{13}{9}}$
= ${\dfrac{13\times 9}{5\times 9}+\dfrac{13\times 5}{9\times 5}}$
= ${\dfrac{117}{45}+\dfrac{65}{45}}$
= ${\dfrac{117+65}{45}}$
= ${\dfrac{182}{45}}$
= ${4\dfrac{2}{45}}$