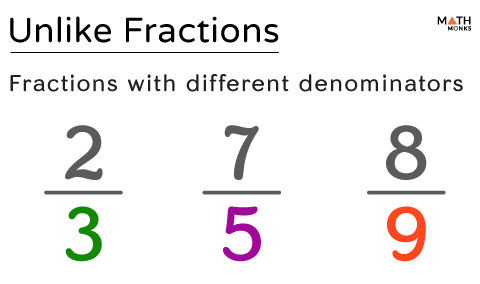Unlike Fractions

Unlike Fractions are the types of fractions with different denominators. 

${\dfrac{2}{3}}$, ${\dfrac{7}{5}}$, and ${\dfrac{8}{9}}$ are a few examples of unlike fractions.

To carry out any operation involving unlike fractions, first, we convert them into like fractions and then perform the given operation. 

Converting Unlike to Like Fractions

To convert unlike fractions to like fractions, we find the least common multiple of the given fractions and then their equivalent fractions with the least common multiple as their denominator. 

Let us convert the unlike fractions ${\dfrac{2}{7}}$, ${\dfrac{3}{2}}$, and ${\dfrac{4}{3}}$ into like fractions.

For finding the least common multiple (LCM) of the denominators:

Here, the denominators are 7, 2, and 3

The LCM of 7, 2, and 3 is 42

Now, for finding their equivalent fractions with denominator 42 

${\dfrac{2\times 6}{7\times 6}=\dfrac{12}{42}}$

${\dfrac{3\times 21}{2\times 21}=\dfrac{63}{42}}$

${\dfrac{4\times 14}{3\times 14}=\dfrac{56}{42}}$

Thus, their corresponding like fractions are: ${\dfrac{12}{42}}$, ${\dfrac{63}{42}}$, and ${\dfrac{56}{42}}$

Comparing

To compare two or more unlike fractions, we first convert them to like fractions and then compare. 

With Same Numerators

Here, the fraction with the greater denominator is the smallest, while the one with the smaller denominator is the largest.

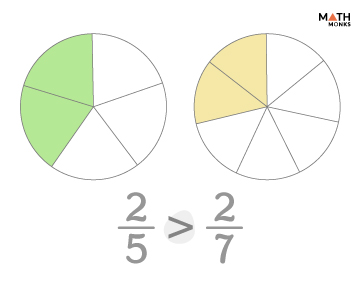
Now, let us compare ${\dfrac{2}{7}}$ and ${\dfrac{2}{5}}$

Here, the numerators are the same, which is 2

Since ${\dfrac{2}{5}}$ has the smaller denominator, ${\dfrac{2}{5}}$ > ${\dfrac{2}{7}}$

This can be represented using a bar model. 

With Different Numerators

1. By Cross Multiplication

This method is used to compare any two given fractions. 

Here, we multiply the numerator of one fraction with the denominator of the other and then compare their products in the same order.

To compare ${\dfrac{5}{3}}$ and ${\dfrac{2}{7}}$

By cross-multiplying, we get

7 × 5 > 2 × 3  ⇒ 6 < 35

Thus, ${\dfrac{5}{3}}$ > ${\dfrac{2}{7}}$

2. By Finding the Least Common Multiple

Here, we convert the unlike fractions to like fractions and then compare.

Let the given fractions are ${\dfrac{2}{7}}$ and ${\dfrac{5}{3}}$

The LCM of their denominators is 21

Now, calculating their equivalent fractions with the same denominator, 

${\dfrac{2\times 3}{7\times 3}=\dfrac{6}{21}}$

${\dfrac{5\times 7}{3\times 7}=\dfrac{35}{21}}$

Comparing the numerators, 

35 > 6

Thus, 

${\dfrac{35}{21}}$ > ${\dfrac{6}{21}}$

Adding and Subtracting

To add two or more unlike fractions, we first convert them to like fractions and add them. 

For adding ${\dfrac{3}{5}+\dfrac{1}{4}}$

Here, the denominators are 5 and 4, and their LCM is 20 

= ${\dfrac{3\times 4}{5\times 4}+\dfrac{1\times 5}{4\times 5}}$

= ${\dfrac{12}{20}+\dfrac{5}{20}}$

= ${\dfrac{12+5}{20}}$

= ${\dfrac{17}{20}}$

Similarly, let us subtract ${\dfrac{1}{4}}$ from ${\dfrac{3}{5}}$

${\dfrac{3}{5}-\dfrac{1}{4}}$

= ${\dfrac{3\times 4}{5\times 4}-\dfrac{1\times 5}{4\times 5}}$

= ${\dfrac{12}{20}-\dfrac{5}{20}}$

= ${\dfrac{12-5}{20}}$

= ${\dfrac{7}{20}}$

Multiplying and Dividing

To multiply two or more unlike fractions, we multiply the numerators and the denominators separately and then convert their product into its simplest form when necessary. 

Let us now multiply ${\dfrac{4}{3}\times \dfrac{2}{5}}$

${\dfrac{4}{3}\times \dfrac{2}{5}}$

= ${\dfrac{4\times 2}{3\times 5}}$

= ${\dfrac{8}{15}}$

To divide a like fraction by another like fraction, we multiply the first fraction by the reciprocal of the second.

For dividing ${\dfrac{4}{3}\div \dfrac{2}{5}}$

${\dfrac{4}{3}\div \dfrac{2}{5}}$

= ${\dfrac{4}{3}\times \dfrac{5}{2}}$

= ${\dfrac{4\times 5}{3\times 2}}$

= ${\dfrac{20}{6}}$

= ${\dfrac{10}{3}}$

Solved Examples