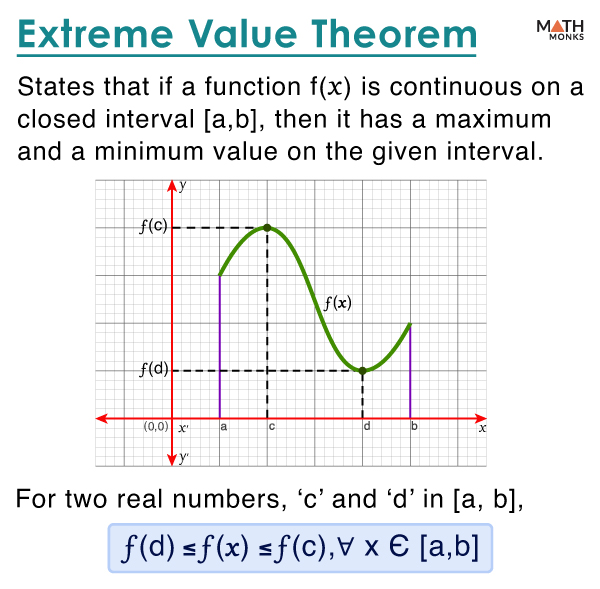
The extreme value theorem states that if a function f(x) is continuous on a closed interval [a, b], it has a maximum and a minimum value on the given interval. It is thus used in real analysis for finding a function’s possible maximum and minimum values on certain intervals.
Here, in the graph, if f(x) is a continuous function on [a, b], then two real numbers, ‘c’ and ‘d,’ exist on [a, b] such that f(c) is the maximum value and f(d) is the minimum value of the given function.
Mathematically, it is written by the formula f(d) ≤ f(x) ≤ f(c), ∀ x Є [a, b], which is graphically represented as:
Proof
It is a two-step process. The first step involves verifying the existence of the maximum value and then verifying the existence of the minimum value.
Existence of Maximum Value
First, we will prove that a point ‘c’ exists on [a, b] such that f(c) is the maximum value of f(x) on [a, b].
Since f(x) is continuous and bounded on [a, b], there exists ‘m’ and ‘M’ such that m ≤ f(x) ≤ M
Let ‘M’ be the least upper bound of f(x)
Now, considering the set S = {x Є [a, b]: f(x) = M}, where f(x) attains its maximum value on [a, b], ‘S’ is non-empty and bounded above by ‘b.’
By the completeness property of real numbers, ‘S’ has the least upper bound, say ‘c.’
Let us assume f(c) < M
By continuity of f(x), for any ε > 0, there exists a δ > 0 such that |f(x) – f(c)| < ε whenever |x – c| < δ
Choosing ε = M – f(c), we have f(x) > f(c), which contradicts the maximality of ‘M.’
Similarly, if f(c) > M, we get f(x) > f(c), which contradicts the maximality of ‘M.’
Thus, f(c) = M, and ‘c’ is a point where f(x) has its maximum value on [a, b].
Existence of Minimum Value
Now, let us consider a set T = {x Є [a, b]: f(x) = m}, here ‘m’ is the minimum value of f(x) on [a, b]
Since f(x) is continuous, ‘T’ is non-empty, and ‘T’ is bounded below by ‘a.’
By the completeness property of real numbers, ‘T’ has the greatest lower bound, say ‘d.’
Let us assume f(d) > m
By continuity of f(x), for any ε > 0, there exists a δ > 0 such that |f(x) – f(d)| < ε whenever |x – d| < δ
Choosing ε = f(d) – m, we have f(x) < f(d), which contradicts the minimality of ‘m.’
Similarly, if f(d) < m, we get f(x) < f(d), which contradicts the minimality of ‘m.’
Thus, f(d) = m, and d is a point where f(x) has its minimum value on [a, b].
Solved Example
![]()
Use the extreme value theorem to find the maximum and minimum values of f(x) = x3 + 12x2 – 14 on [-2, 2] and explain the results.
Solution:
![]()
Since the polynomial function f(x) is differentiable on [-2, 2], f(x) is continuous.
Differentiating f(x) with respect to x, we get f’(x) = 3x2 + 24x
Since [-2, 2] is closed and bounded, applying the extreme value theorem, we get:
f’(x) = 0
⇒ 3x2 + 24x = 0
⇒ 3x(x + 8) = 0
⇒ either x = -8 or x = 0
Thus, -8 and 0 are the critical points.
Now, finding the values of f(x) at the critical points and the endpoints of [-2, 2], we get
f(-8) = (-8)3 + 12(-8)2 – 14 = 242
f(0) = (0)3 + 12(0)2 – 14 = -14
f(-2) = (-2)3 + 12(-2)2 – 14 = 26
f(2) = (2)3 + 12(2)2 – 14 = 42
Thus, the minimum value of f(x) on [-2, 2] is -14, and the maximum value of f(x) on [-2, 2] is 242.
