5 Ways to Prove a Quadrilateral is a Parallelogram

This article will help us learn how to prove something is a parallelogram. More precisely, how to prove a quadrilateral is a parallelogram.

There are 5 basic ways to prove a quadrilateral is a parallelogram. They are as follows:

1. Proving opposite sides are congruent
2. Proving opposite sides are parallel
3. Proving the quadrilateral’s diagonals bisect each other
4. Proving opposite angles are congruent
5. Proving consecutive angles are supplementary (adding to 180°)

Let us now prove the above statements one by one.

1) Proving Opposite Sides are Congruent

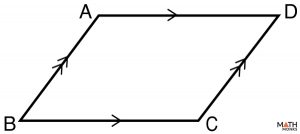
Prove that opposite sides of a parallelogram are congruent

To prove: AB ≅ CD, AD ≅ BC

Proof:

Given: AB ∥ CD, AD ∥ BC

Draw in a diagonal AC

Statement	Reason
∠ACB ≅ ∠CAD	Alternate interior angles
∠BAC ≅ ∠ACD	Alternate interior angles
AC ≅ AC	Common side (identity)
ΔADC ≅ ΔABC	Angle-Angle-Side (AAS) postulate
AD ≅ BC AB ≅ CD	Corresponding Parts of Congruent Triangles are Congruent (CPCTC) Hence Proved

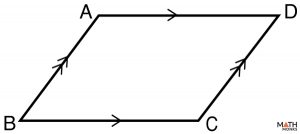
2) Proving Opposite Sides are Parallel

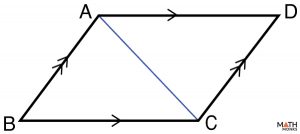
Prove that opposite sides of a parallelogram are parallel

To prove: AB ∥ CD, AD ∥ BC

Proof:

Given: AB ≅ CD, AD ≅ BC

Draw in a diagonal AC

Statement	Reason
AC ≅ AC	Common side (identity)
ΔADC ≅ ΔABC	SSS postulate
∠ACB ≅ ∠CAD	CPCTC
∠BAC ≅ ∠ACD	CPCTC
AB ∥ CD	Alternate interior angles Hence Proved
AD ∥ BC	Alternate interior angles Hence Proved

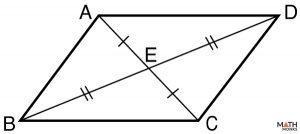
3) Proving Diagonals Bisect Each Other

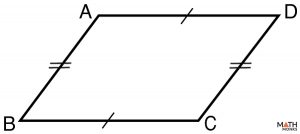
Prove that the diagonals of a parallelogram bisect each other.

This is an “if and only if” proof, so there are two things to prove.

1. To prove: AE ≅ EC, BE ≅ ED

Proof:

Given: ABCD is a parallelogram

Statement	Reason
AD ∥ BC	Definition of parallelogram
∠DAE ≅ ∠BCE	Alternate interior angles
ADE ≅ CBE	Alternate interior angles
AD ≅ BC	Opposite sides of parallelogram
ΔADC ≅ ΔABC	AAS postulate
AE ≅ EC	CPCTC Hence Proved
BE ≅ ED	CPCTC Hence Proved

And the converse

2. To prove: ABCD is a parallelogram

Proof:

Given: AE ≅ EC, BE ≅ ED

Statement	Reason
∠AED ≅ ∠BEC	Vertical angles
∠AEB ≅ ∠CED	Vertical angles
ΔADC ≅ ΔABC	AAS
AD ≅ BC	CPCTC
AB ≅ CD	CPCTC
ABCD is a parallelogram	Theorem 2 Hence Proved

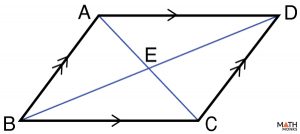
4) Proving Opposite Angles are Congruent

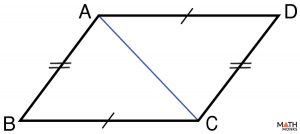
Prove that the opposite angles of a parallelogram are congruent.

To prove: ∠ADC ≅ ∠ABC, ∠BAD ≅  ∠BCD

Proof:

Given: AB ∥ CD, AD ∥ BC

Draw in a diagonal AC

Statement	Reason
∠ACB ≅ ∠CAD	Alternate interior angles
∠ADB ≅ ∠CBD	Alternate interior angles
∠AED ≅ ∠BEC	Vertical angles
∠AEB ≅ ∠CED	Vertical angles
ΔADC ≅ ΔABC	AAS postulate
ΔBAD ≅  ΔBCD	AAS postulate
∠ADC ≅ ∠ABC	CPCTC postulate Hence Proved
∠BAD ≅  ∠BCD	CPCTC postulate Hence Proved

5) Proving Consecutive Angles are Supplementary

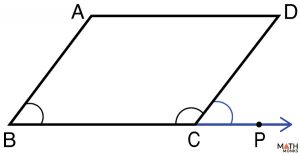
Prove that the consecutive angles of a parallelogram are supplementary (add up to 180°).

To prove: ∠ABC + ∠BCD = 180°

Proof:

Given: AB ∥ CD, AD ∥ BC

Extend BC till P

Statement	Reason
∠ABC ≅ ∠DCP	Corresponding angle
∠BCD + ∠DCP = 180°	Linear angle
∠ABC + ∠BCD = 180°	∠ABC ≅ ∠DCP Hence Proved