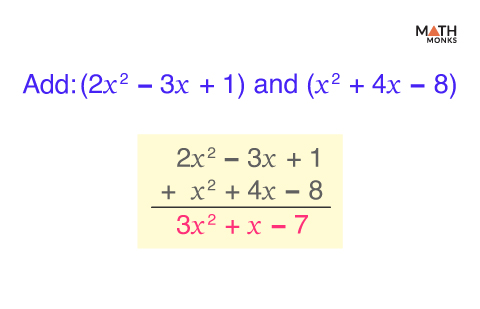Adding and Subtracting Polynomials

When adding or subtracting polynomials, we simply add the like terms. Like terms in polynomials are terms with the same variable raised to the same power. 

For example, in the expression 3x² + 5x + x², the terms 3x² and x² are like terms as they both involve x raised to the power of 2. 

With Different Degrees

When adding or subtracting polynomials with different degrees, we arrange the terms by degree and align the like terms. If a term in one polynomial does not have a corresponding term in the other, the result remains unchanged.

For example, to add (3x² + x + 1) and (x³ + x² + 4), we simply align the terms of each polynomial based on their degrees:

(0x³ + 3x² + x + 1) + (x³ + x² + 0x + 4) = x³ + 4x² + x + 5

Addition and subtraction can be done either by arranging the polynomials side by side or horizontally (horizontal method) or one above the other (vertical method). 

By Horizontal Method

Adding 

In this method, we write the polynomials next to each other and combine the like terms by adding their coefficients.

Let us add the polynomials (4x² – x + 3) and (x² + 2x + 5) 

Writing the Polynomials Next to Each Other

(4x² – x + 3) + (x² + 2x + 5)

= 4x² – x + 3 + x² + 2x + 5

Combining the Like Terms

= (4x² + x²) + (-x + 2x) + (3 + 5)

= 5x² + x + 8

Thus, the sum is 5x² + x + 8

Here is another example of adding polynomials (2x² – 3x + 1) and (x² + 4x – 8)

Subtracting

For subtracting polynomials, we first write the polynomials next to each other, distribute the subtraction sign (due to which ‘+’ changes to ‘-’ and ‘-’ changes to ‘+’), and then combine the like terms by subtracting their coefficients.

Let us subtract the polynomial (x² + 2x + 5) from (4x² – x + 3)

Writing the Polynomials Next to Each Other

(4x² – x + 3) – (x² + 2x + 5)

Distributing the Subtraction Sign

= 4x² – x + 3 – x² – 2x – 5

Combining the Like Terms

= (4x² – x²) + (-x – 2x) + (3 – 5)

= 3x² – 3x – 2

Thus, the difference is 3x² – 3x – 2

Here is another example of adding polynomials (5x³ – 8x² + 2) and (x² – x – 1)

By Vertical Method

Adding 

In this method, we arrange each polynomial term in a column, align the like terms, and then add each column.

To add (4x² – x + 3) and (x² + 2x + 5) using the vertical method, we follow the following steps. 

Arranging the Like Terms Vertically

${\begin{aligned}4x^{2}-x+3\\ \dfrac{+x^{2}+2x+5}{}\end{aligned}}$

Adding Each Column

${\begin{aligned}4x^{2}-x+3\\ \dfrac{+x^{2}+2x+5}{5x^{2}+x+8}\end{aligned}}$

Thus, the sum is 5x² + x + 8

Here is another example of adding polynomials (2x² – 3x + 1) and (x² + 4x – 8)

Subtracting

In this method, we arrange the polynomials vertically, change the signs of each term in the second polynomial (‘+’ changes to ‘-’ and ‘-’ changes to ‘+’), and then combine each column.

Let us subtract (x² + 2x + 5) from (4x² – x + 3) 

Arranging the Like Terms Vertically 

${\begin{aligned}4x^{2}-x+3\\ \dfrac{-\left( x^{2}+2x+5\right) }{}\end{aligned}}$

Changing the Signs

${\begin{aligned}4x^{2}-x+3\\ \dfrac{-x^{2}-2x-5}{}\end{aligned}}$

Evaluating Each Column

${\begin{aligned}4x^{2}-x+3\\ \dfrac{-x^{2}-2x-5}{3x^{2}-3x-2}\end{aligned}}$

Thus, the difference is 3x² – 3x – 2

Here is another example of adding polynomials (5x³ – 8x² + 2) and (x² – x – 1)

Note: 

• We must distribute the negative sign during subtraction and combine the terms with different exponents
• We must double-check that all the like terms are combined correctly and all signs are distributed as required.

Solved Examples