Multiplying Polynomials

There are various methods to multiply polynomials, depending on their types. 

To multiply two polynomials, we follow the following steps:

1. Multiplying Each Term in One Polynomial by Each Term in the Other Polynomial
2. Adding the Resulting Terms Together 
3. Simplifying (if needed)

Degree of the Product

If P(x) and Q(x) are two polynomials, the degree of the product will always be higher than the degree of P(x) or Q(x). The degree of the resulting polynomial is the sum of the degrees of P(x) and Q(x).

Mathematically, 

Degree(P ⋅ Q) = Degree(P) + Degree(Q)

Monomial by Monomial

When multiplying a monomial by another monomial, we first multiply the constants and the variables separately and then combine the results.

Let us multiply 3x ⋅ 6xy 

Multiplying Constants and Variables

= (3 ⋅ 6)(x ⋅ xy)

= (18)(x²y)

Combining the Result

= 18x²y

Monomial by Binomial

When multiplying a binomial by a monomial, we multiply each of the two terms in the binomial by the monomial and then add the results.

Let us multiply 6xy(x + 7)

Here, we will use the distributive property, which states that a(b + c) = ab + ac

Multiplying Each Term in Binomial by Monomial

6xy ⋅ x = 6(x ⋅ xy) = 6x²y

6xy ⋅ 7 = (6 ⋅ 7)xy = 42xy

Adding the Resulting Terms

Thus, 6xy(x + 7) = 6x²y + 42xy

Binomial by Binomial

When multiplying a binomial by another binomial, there are two common approaches:

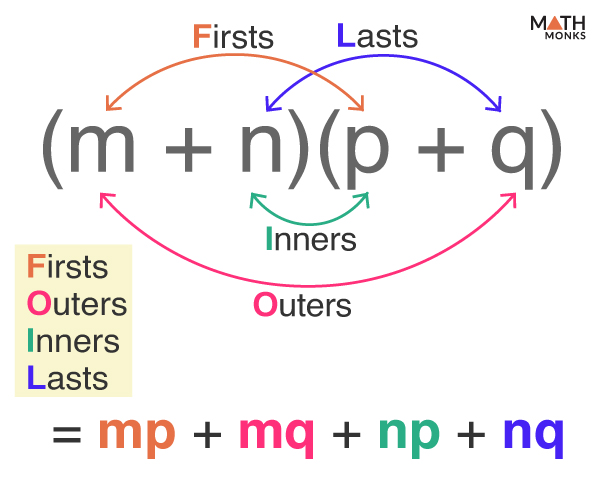
By Distributive Property (FOIL Method)

The distributive property can also be used to multiply two or more binomials or polynomials.

Let us multiply two binomials (m + n) and (p + q)

(m + n)(p + q)

Multiplying Each Term in One Binomial by Each Term of the Other Binomial 

= m(p + q) + n(p + q)

Adding the Resulting Terms 

= mp + mq + np + nq

We can multiply polynomials in any order as long as each term in the first polynomial is multiplied by each term in the second binomial. 

We can remember the steps by ‘FOIL’ (Firsts, Outers, Inners, Lasts)

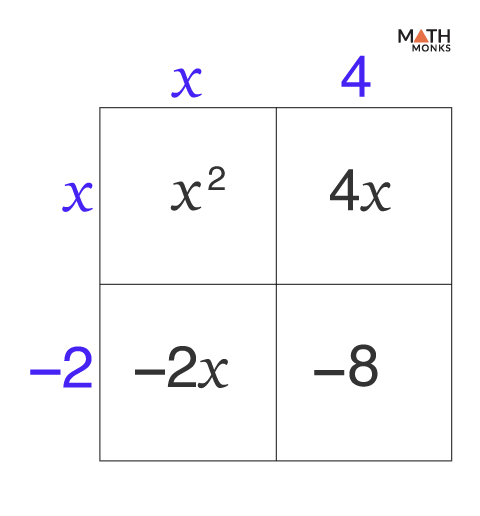
By Box Method

Two binomials can also be multiplied using the box method. In this method, we first write the terms of each polynomial along the top and side of a box and then fill it with the products of the corresponding terms.

The terms are written across a box, and their corresponding products are written inside the box. This method is also known as the lattice method.

Let us multiply (x – 2) by (x + 4)

Forming the Box

Writing each term of the polynomials (x – 2) horizontally and (x + 4) vertically. 

Multiplying the Corresponding Terms

After multiplying the corresponding terms, we get:

Adding the Resulting Terms

Here, the product  is x² + 4x – 2x + 8 = x² + 2x + 8

Thus, the above multiplication method is known as the box multiplication of two binomials.

Polynomial by Polynomial

When multiplying a polynomial by a polynomial, we multiply each term of the first polynomial by each term of the other polynomial and then add them to get the results.

Let us multiply (x² + x – 1) by (2x² – x + 7)

(x² + x – 1)(2x² – x + 7)

Multiplying Each Term of the First Polynomial by the Other

= x²(2x² – x + 7) + x(2x² – x + 7) – 1(2x² – x + 7)

Adding the Resulting Terms 

= 2x⁴ – x³ + 7x² + 2x³ – x² + 7x – 2x² + x – 7

= 2x⁴ + (-x³ + 2x³) + (7x² – x² – 2x²) + (7x + x) – 7

Simplifying

= 2x⁴ + x³ + 4x² + 8x – 7

Thus, (x² + x – 1)(2x² – x + 7) = 2x⁴ + x³ + 4x² + 8x – 7