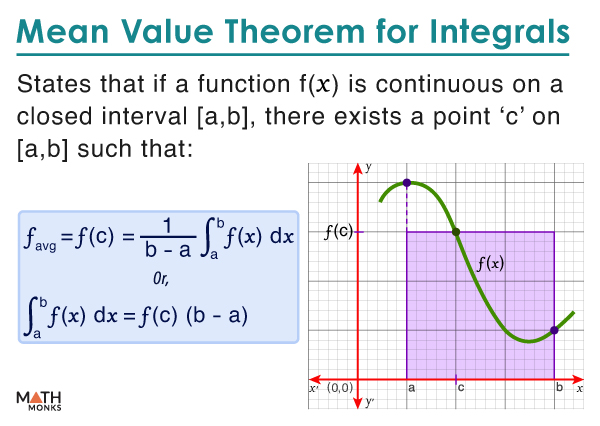
The mean value theorem for integrals states that if a function f(x) is continuous on a closed interval [a, b], there exists a point ‘c’ on [a, b] such that f(x) at c equals the average value of f(x) on the given interval.
Mathematically, it is generalized as,
${f\left( c\right) =\dfrac{1}{b-a}\int ^{b}_{a}f\left( x\right) dx}$
or,
${\int ^{b}_{a}f\left( x\right) dx=f\left( c\right) \left( b-a\right)}$
In the above graph, the shaded rectangular part of the curve is the average value of the function f(x).
Proof
Since f(x) is continuous on [a, b]
By the extreme value theorem, f(x) attains its minimum and maximum values.
Let ‘m’ and ‘M’ be the minimum and the maximum values on [a, b]
Thus, ∀ x Є [a, b], m ≤ f(x) ≤ M
Now, by the comparison theorem, we get
${m\left( b-a\right) \leq \int ^{b}_{a}f\left( x\right) dx\leq M\left( b-a\right)}$
On dividing by (b – a), we get
${m\leq \dfrac{1}{\left( b-a\right) }\int ^{b}_{a}f\left( x\right) dx\leq M}$
Since f(x) is continuous on [a, b] and ${m\leq \dfrac{1}{\left( b-a\right) }\int ^{b}_{a}f\left( x\right) dx\leq M}$, for m, M Є [a, b], then by the intermediate value theorem, a number ‘c’ exists on [a, b] such that
${f\left( c\right) =\dfrac{1}{b-a}\int ^{b}_{a}f\left( x\right) dx}$
⇒ ${\int ^{b}_{a}f\left( x\right) dx=f\left( c\right) \left( b-a\right)}$
Hence, the mean value theorem for integrals is proved.
This relationship can also be represented as:
If f(x) is integrable on [a, b], the average value of f(x) on [a, b] is ${f_{avg}=\dfrac{1}{b-a}\int ^{b}_{a}f\left( x\right) dx}$
Solved Examples
![]()
Find the point ‘c’ to satisfy the mean value theorem for the integrals of a function f(x) = 12x – 8 on [2, 6].
Solution:
![]()
Since f(x) = 12x – 8 is a polynomial, it is continuous on [2, 6]
By the mean value theorem for integrals, we get
${\int ^{b}_{a}f\left( x\right) dx=f\left( c\right) \left( b-a\right)}$
⇒ ${\int ^{6}_{2}\left( 12x-8\right) dx=\left( 12c-8\right) \left( 6-2\right)}$
⇒ ${12\int ^{6}_{2}xdx-8\int ^{6}_{2}dx=48c-32}$
⇒ ${12\left[ \dfrac{6^{2}}{2}-\dfrac{2^{2}}{2}\right] -8\left[ 6-2\right] =48c-32}$
⇒ ${6\times 32-8\times 4=48c-32}$
⇒ 48c = 192
⇒ c = 4 Є [2, 6]
Thus, the only solution of ‘c’ is 4.
![]()
Find the average value of f(x) = 3x2 – 5x on [0, 4] and find ‘c’ such that f(c) = favg on [0, 4].
Solution:
![]()
Since f(x) = 3x2 – 5x is a polynomial, it is continuous on [0, 4]
By the mean value theorem for integrals, we get
${f\left( c\right) =\dfrac{1}{b-a}\int ^{b}_{a}f\left( x\right) dx}$
⇒ ${f\left( c\right) =\dfrac{1}{4-0}\int ^{4}_{0}\left( 3x^{2}-5x\right) dx}$
⇒ ${f\left( c\right) =\dfrac{1}{4}\int ^{4}_{0}3x^{2}dx-\dfrac{5}{4}\int ^{4}_{0}xdx}$
⇒ ${f\left( c\right) =\dfrac{1}{4}\left[ \left( 4\right) ^{3}-\left( 0\right) ^{3}\right] -\dfrac{5}{4}\left[ \dfrac{\left( 4\right) ^{2}}{2}-\dfrac{\left( 0\right) ^{2}}{2}\right]}$
⇒ ${f\left( c\right) =\dfrac{1}{4}\times 64-\dfrac{5}{4}\times \dfrac{16}{2}}$
⇒ ${f\left( c\right) =16-10}$
⇒ ${f\left( c\right) =6}$, which is the average value of f(x) on [0, 4].
Now, f(c) = 3c2 – 5c = 6
⇒ 3c2 – 5c – 6 = 0
On applying the quadratic formula, we get
either c = ${\dfrac{5+\sqrt{97}}{6}}$ or c = ${\dfrac{5-\sqrt{97}}{6}}$
Approximating the value of ${\sqrt{97}}$ up to 3 decimal places, we get c = 2.475 or -0.808, respectively.
Since c = 2.475 Є [0, 4], the value of c is 2.475
Thus, the average value of f(x) = f(c) = 6, and the value of ‘c’ is approximately 2.475 on [0, 4].
