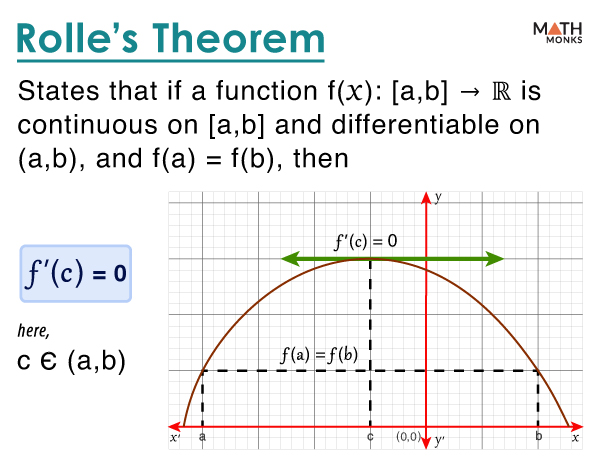
Rolle’s Theorem

Rolle’s theorem is a theorem in calculus that states if a function ‘f’ is continuous on the closed interval [a, b], differentiable on the open interval (a, b), and f(a) = f(b), then there exists at least one point c Є (a, b), such that f’(c) = 0.

Mathematically, 

Let f(x): [a, b] → ℝ be continuous on [a, b] and differentiable on (a, b) 

If f(a) = f(b), then

f’(c) = 0, where c Є (a, b)

Thus, Rolle’s Theorem states that if a function has 2 points (a, f(a)) and (b, f(b)) on a graph with the same y-coordinate, then there is at least one relative minimum or maximum between these points where the function ‘turns around’ and the first derivative is 0 at that point.

Thus, it is a special case of Lagrange’s mean value theorem (MVT).

Graphing

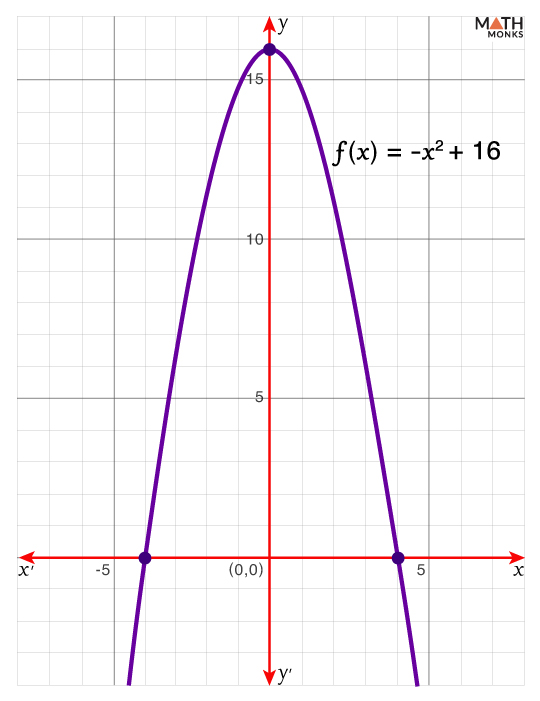
Let us plot the function f(x) = -x² + 16 on [-4, 4].

In the above graph, since the curve is smooth on [4, -4] with no breaks or jumps, f(x) is continuous and differentiable within the interval. Also, f(-4) and f(4) cuts the x-axis, which means the two points (-4, f(-4)) and (4, f(4)) have the same y-coordinate.

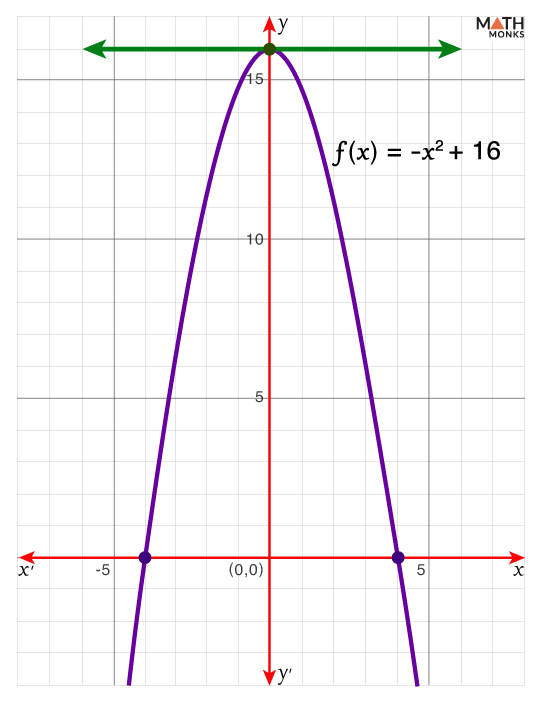
By Rolle’s theorem, we get at least one relative minimum or maximum between the points (-4, f(-4)) and (4, f(4)) where the function is turning around.

Here, at x = 0 (-4 < 0 < 4), f(x) turns around.

Thus, it is possible to draw a horizontal tangent line at x = 0 and f(0) = 16 where f’(0) = 0.

Proof

Case 1: When ‘f’ is Constant

Since ‘f’ is continuous on [a, b], from the extreme value theorem, ‘f’ attains the maximum and minimum values on [a, b]. 

Also, since ‘f’ is differentiable on (a, b), f’(c) exists for c Є (a, b). If this occurs at the endpoints ‘a’ and ‘b,’ then f(x) is a constant function on [a, b], and f’(x) = 0 at any point.

Thus, at any point c Є (a, b), f’(c) = 0, Rolle’s theorem holds.

Case 2: When ‘f’ is Not Constant

Now, let us suppose that f(x) is not a constant function on [a, b]. This implies there exists at least one point where f(x) attains a maximum or minimum value on (a, b).

Now, considering f(x) attains its maximum and minimum value at an interior point ‘c’ on (a, b), we get:

Since the derivative is zero or undefined at both maximum and minimum points, then for f(x) attaining its maximum value or minimum value at ‘c,’ f’(c) = 0

Let us suppose that f(x) reaches its maximum and minimum values at an endpoint ‘a’ or ‘b.’ If f(x) attains its maximum value at ‘a’ without any loss of generality and f(a) = f(b), then f(x) attains its maximum value at ‘b.’ 

Hence, ‘f’ is a constant function on [a, b], and Rolle’s theorem holds.

In either case, we find at least one point ‘c’ on (a, b) such that f’(c) = 0.

Thus, Rolle’s theorem is proved.

Rolle’s theorem can also be proved using Lagrange’s mean value theorem. 

Alternative Method

Let the function ‘f’ be differentiable on (a, b) and continuous on [a, b]

If f(a) = f(b)

By Lagrange’s mean value theorem, we get

${f’\left( c\right) =\dfrac{f\left( b\right) -f\left( a\right) }{b-a}}$

⇒ ${f’\left( c\right) =\dfrac{f\left( b\right) -f\left( b\right) }{b-a}}$

⇒ ${f’\left( c\right) =\dfrac{0}{b-a}}$

⇒ ${f’\left( c\right) =0}$

Thus, Rolle’s theorem is proved.

Finding Roots

Let us apply Rolle’s theorem to find the roots of a polynomial function f(x) = x³ – 3x² + 2x on [0, 2].

Since f(x) is a polynomial function, ‘f’ is continuous and differentiable at any interval, which satisfies the conditions of Rolle’s theorem.

Now, evaluating f(0) and f(2), we get

f(0) = (0)³ – 3(0)² + 2(0) = 0

f(2) = (2)³ – 3(2)² + 2(2) = 0

Thus, f(0) = f(2) = 0

By Rolle’s theorem, there exists at least one point c Є (0, 2), f’(c) = 0

Now, we find ‘c’ such that f’(c) = 0

Finding the derivative of f(x), we get

f’(x) = 3x² – 6x + 2

Putting f’(x) = 0, we get

3x² – 6x + 2 = 0

Using the quadratic formula, we get

${x=\dfrac{-\left( -6\right) \pm \sqrt{\left( -6\right) ^{2}-4\times 3\times 2}}{2\times 3}}$

⇒ ${x=\dfrac{6\pm \sqrt{12}}{6}}$

⇒ ${x=\dfrac{3\pm \sqrt{3}}{3}}$

Here, x ≈ 1.577 and x ≈ 0.423, and both the roots are within (0, 2)

Thus, By Rolle’s theorem, we get two roots of f(x) = x³ – 3x² + 2x on [0, 2], specifically at x ≈ 1.577 and x ≈ 0.423

Solved Examples