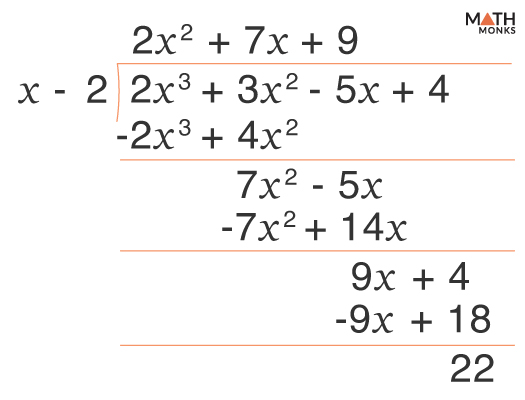Just like dividing numbers, we can also divide one polynomial (the dividend) by another polynomial (the divisor), resulting in a quotient and sometimes a remainder. The degree of the divisor is always less than that of the dividend.
For example,
All polynomials can be divided either by long division or by synthetic division method. However, when a polynomial is divided by a monomial, we will be using the factoring method or splitting the terms for simplicity, as shown in the next section.
Dividing Polynomials by Monomials
When dividing a polynomial by a monomial, we can use two methods: factoring or splitting the terms.
By Factoring
In the factoring method, we first factor out the common terms in the polynomial. We then divide the numerator by the common factor to obtain the quotient.
Let us divide the polynomial ${\dfrac{2x^{2}-x}{x}}$
Taking the Common Factors Out
= ${\dfrac{x\left( 2x-1\right) }{x}}$
Cancelling
= ${\left( 2x-1\right)}$
Thus, the quotient is 2x – 1
By Splitting the Terms
In the splitting method, each term in the numerator is divided by the denominator individually and then simplified.
Let us divide the polynomial ${\dfrac{2x^{2}-x}{x}}$
Splitting the Terms
= ${\dfrac{2x^{2}}{x}-\dfrac{x}{x}}$
Simplifying
Using the quotient rule in each term,
= 2x2 – 1 – x1 – 1
= 2x1 – x0
Using one-exponent and zero-exponent property,
= 2x – 1
Thus, the quotient is 2x – 1
Dividing Polynomials by Polynomials
To divide a polynomial by another polynomial (except a monomial), we can use either the long division method or synthetic division.
By Long Division
Polynomial long division resembles numeric long division. We divide the leading term of the dividend by the leading term of the divisor, subtract the result, bring down the next term, and repeat until no further division is possible.
Let us divide the polynomial 3x4 – 4x3 – 3x – 1 by x – 1 using the long division method.
Here, the dividend 3x4 – 4x3 – 3x – 1 will be placed inside the division bracket, and the divisor x – 1 is placed outside. The division is shown below.
- The dividend 3x4 – 4x3 – 3x – 1 is arranged from highest to lowest degree with all missing terms (here, written as 0x2).
- The leading term of the dividend, 3x4, is divided by the leading term of the divisor, x, resulting in 3x3.
- The quotient, 3x3, is then multiplied by the divisor, x – 1. The product is 3x4 – 3x3.
- The product, 3x4 – 3x3, is subtracted from the original dividend. Now, bringing down the next term, we get the new dividend: -x3 + 0x2
- The new leading term, -x3, is divided by x, giving -x2. Now, repeating the same process, we get the new dividend as -x2 – 3x
- Again, repeating the same process, the new dividend becomes -4x – 1
- Further, repeating the same process, the new dividend is -5, which cannot be divided further by x – 1
Thus, the quotient is 3x3 – x2 – x – 4 and the remainder is -5
To learn more about the long division of polynomials, click here.
By Synthetic Division
When dividing a polynomial by a linear divisor of the form x−c, the synthetic division is faster and particularly useful for higher-degree polynomials.
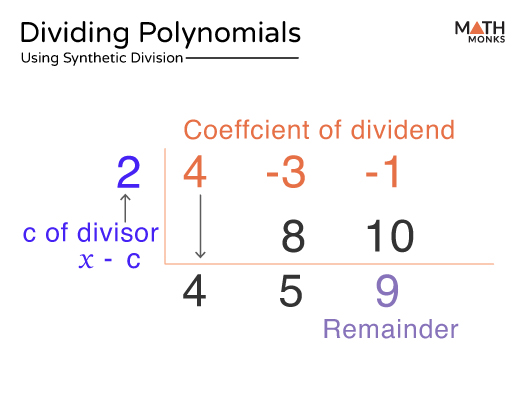
Let us divide the polynomial 4x2 – 3x – 1 by x – 2 using the synthetic method.
- Here, the dividend is 4x2 – 3x – 1. Thus, the coefficients of the dividend (i.e., 4, -3, and -1) are used as the synthetic dividend.
- The divisor is x – 2, so 2 is used as the synthetic divisor.
- Then, we bring down the first coefficient of the dividend, 4, as it is.
- 4 is multiplied by 2. The product is 8 and is placed in the second column.
- 8 is added to the second coefficient of the dividend -3. The sum is 5.
- 5 is multiplied by 2. The product is 10 and is placed in the third column.
- 10 is added to the third coefficient of the dividend -1. The sum is 9
The numbers at the bottom row represent the coefficients of the quotient and the remainder.
Now, we will write the final answer, which will be one degree less than the dividend. Thus, the quotient is 4x + 5, and the remainder is 9
Solved Examples
![]() Divide the polynomial x3 – 2x2 by x – 2 by factoring method
Divide the polynomial x3 – 2x2 by x – 2 by factoring method
Solution:
![]()
Here, ${\dfrac{x^{3}-2x^{2}}{x-2}}$
= ${\dfrac{x^{2}\left( x-2\right) }{x-2}}$
= ${x^{2}}$
Thus, the quotient is ${x^{2}}$
![]() Find the quotient of the cubic polynomial 8x3 – 2x2 + 6x when divided by the monomial 2x
Find the quotient of the cubic polynomial 8x3 – 2x2 + 6x when divided by the monomial 2x
Solution:
![]()
Here, ${\dfrac{8x^{3}-2x^{2}+6x}{2x}}$
= ${\dfrac{8x^{3}}{2x}-\dfrac{2x^{2}}{2x}+\dfrac{6x}{2x}}$
= 4x3 – 1 – x2 – 1 + 3x1 – 1
= 4x2 – x + 3
Thus, the quotient is 4x2 – x + 3
![]() Use the long division method to divide ${\dfrac{2x^{3}+3x^{2}-5x+4}{x-2}}$
Use the long division method to divide ${\dfrac{2x^{3}+3x^{2}-5x+4}{x-2}}$
Solution:
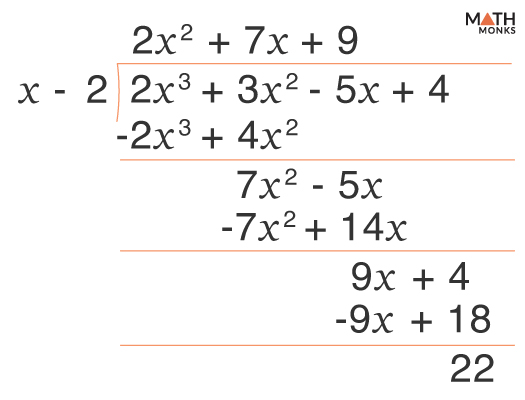
Here, ${\dfrac{2x^{3}+3x^{2}-5x+4}{x-2}}$
Thus, the quotient is 2x2 + 7x + 9, and the remainder is 22
![]() Use synthetic division method to divide ${\dfrac{6x^{3}+10x^{2}-14x+8}{x+3}}$
Use synthetic division method to divide ${\dfrac{6x^{3}+10x^{2}-14x+8}{x+3}}$
Solution:

Here, ${\dfrac{3x^{3}+5x^{2}-7x+4}{x+3}}$
Thus, the quotient is 3x2 – 4x + 5, and the remainder is -11