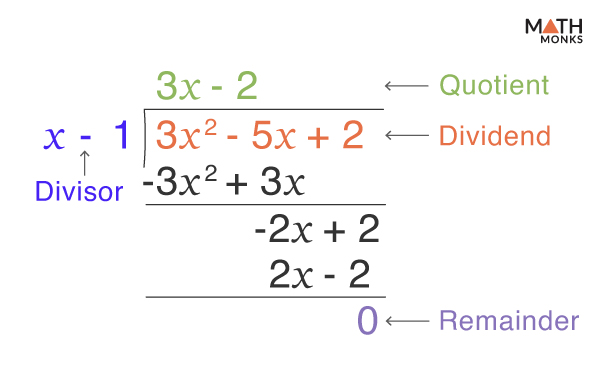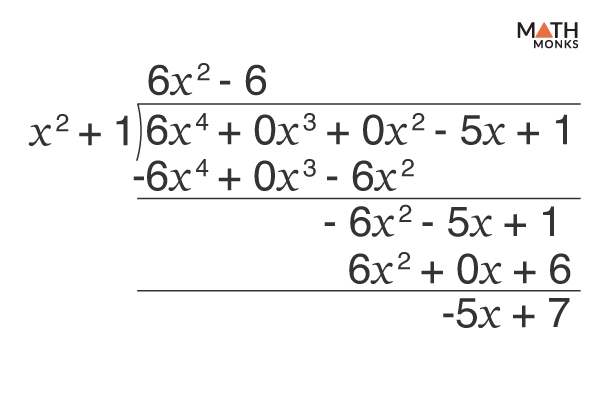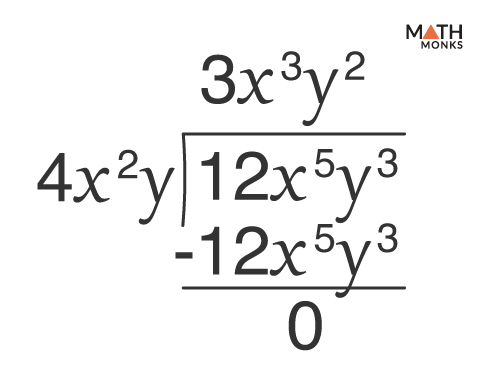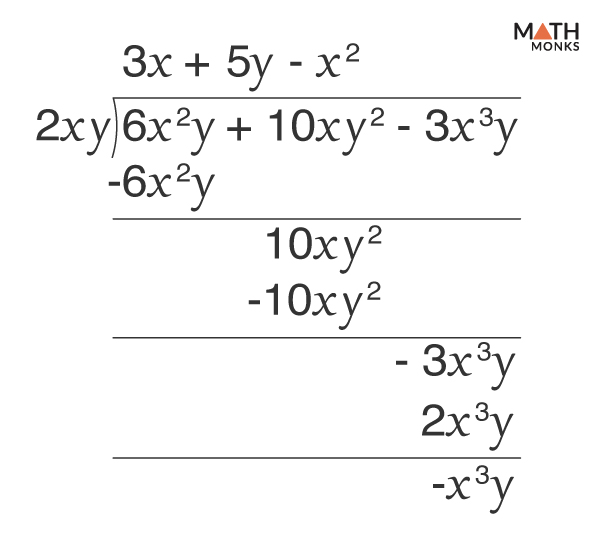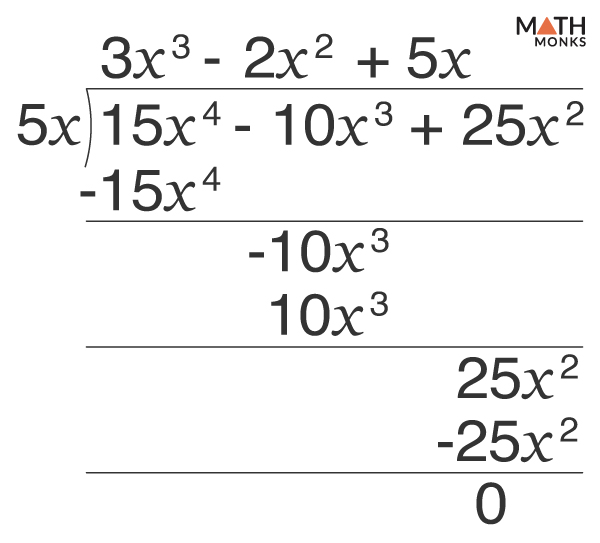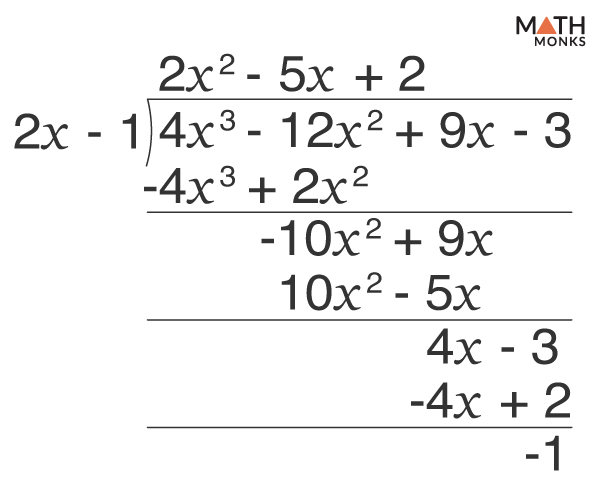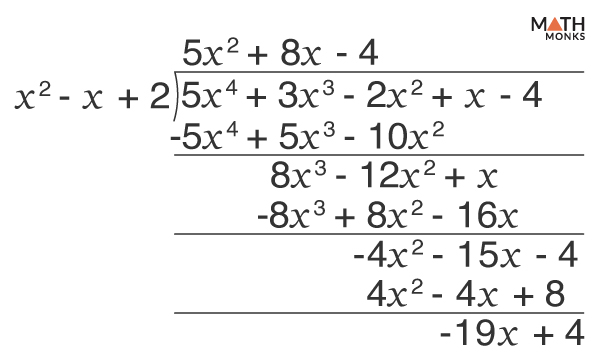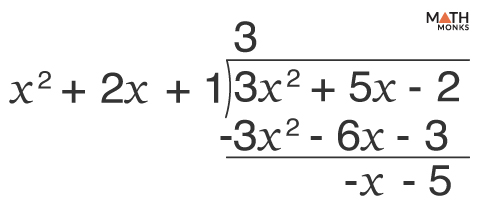Polynomial long division is a method for dividing one polynomial (the dividend) by another (the divisor), which can be a monomial, binomial, or any other polynomial. Similar to numerical division, this method yields a quotient and a remainder.
When written as a fraction, the polynomial in the numerator is the dividend, and the polynomial in the denominator is the divisor.
Steps
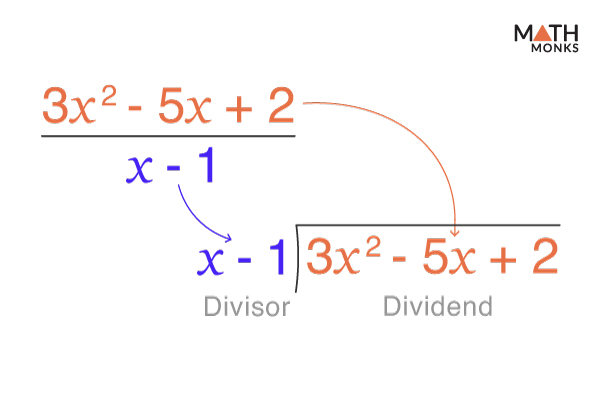
Now, let us divide 3x2 – 5x + 2 by x – 1 using the long-division method.
${\dfrac{3x^{2}-5x+2}{x-1}}$
Arranging Terms of the Dividend
First, we will arrange the terms in the decreasing order of their indices (if required) and write the missing terms of the dividend with a coefficient of 0.
Here, the numerator 3x2 – 5x + 2 and the denominator x – 1 are already arranged in descending order of their indices.
Thus, the dividend is 3x2 – 5x + 2
The divisor is x – 1
Dividing the First Term of the Dividend
On dividing the first term of the dividend 3x2 by the first term of the divisor x, we get
${\dfrac{3x^{2}}{x}=3x}$
Thus, the first term of the quotient is 3x
Multiplying the Result and the Divisor
On multiplying the entire divisor, x – 1, by the result 3x, we get the product
3x(x – 1) = 3x2 – 3x
Subtracting the Product From the Dividend
Now, we subtract the product, 3x2 – 3x, from the dividend, 3x2 – 5x + 2, and bring down the next term, 2. The difference, -2x + 2, along with the brought-down term, 2, will form the new dividend.
On subtracting the product from the dividend and bringing down the next term (i.e., +2), we get the new dividend, which is -2x + 2
Repeating the Steps (Until the Remainder is of Lower Degree)
Now, we will repeat the process until the remainder is either 0 or of a lower degree than the divisor and can no longer be divided.
On repeating the same process, we get
Thus, the quotient is 3x – 2, and the remainder is 0
With Missing Terms
Often, a polynomial expression may have some missing term (for example, there may be a x3, but no x2). In such a case, we either leave gaps or write the missing terms with a coefficient of 0.
Let us divide the 4th-degree polynomial 6x4 – 5x + 1 by the binomial x2 + 1
${\dfrac{6x^{4}-5x+1}{x^{2}+1}}$
Here, the quotient is 6x2 – 6, and remainder is -5x + 7
Problem: Dividing a MONOMIAL by a MONOMIAL
![]()
Divide: ${\dfrac{12x^{5}y^{3}}{4x^{2}y}}$
Solution:
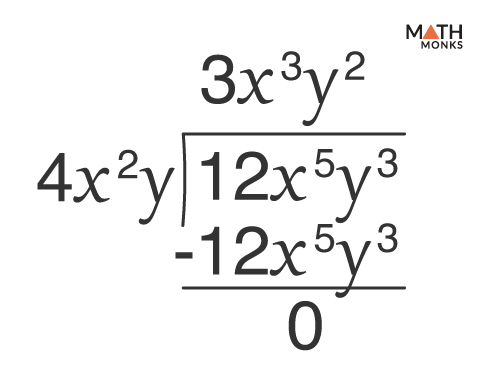
Given, ${\dfrac{12x^{5}y^{3}}{4x^{2}y}}$
Thus, the quotient is 3x3y2
Problem: Dividing a MONOMIAL by a MONOMIAL with TWO or MORE VARIABLES
![]()
Divide: 6x2y + 10xy2 – 3x3y by 2xy
Solution:
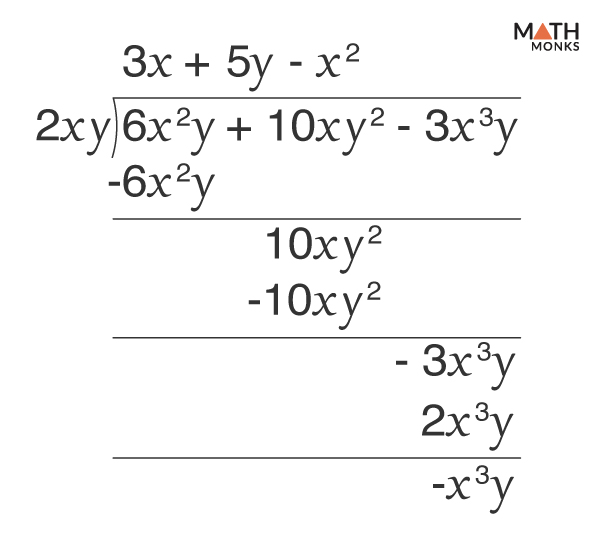
Long division can also be used to divide polynomials with two or more variables (such as when both x and y are present in the expression).
Given, ${\dfrac{6x^{2}y+10xy^{2}-3x^{3}y}{2xy}}$
Thus, the quotient is 3x – 5y – x2, and remainder is -x3y
Problem: Dividing POLYNOMIALS (other than monomials) by a MONOMIAL
![]()
Divide: ${\dfrac{15x^{4}-10x^{3}+25x^{2}}{5x}}$
Solution:
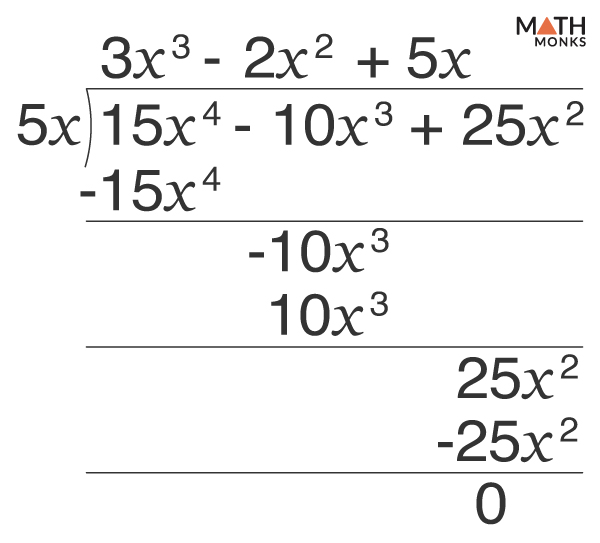
Given, ${\dfrac{15x^{4}-10x^{3}+25x^{2}}{5x}}$
Thus, the quotient is 3x3 – 2x2 + 5x
Problem: Dividing a CUBIC POLYNOMIAL by a polynomial
![]()
Divide a 3rd-degree polynomial 4x3 – 12x2 + 9x – 3 by 2x – 1 and write the quotient in fraction form.
Solution:
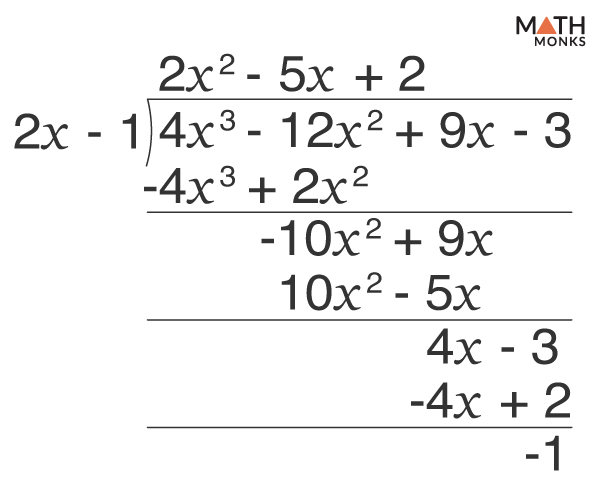
Given, ${\dfrac{4x^{3}-12x^{2}+9x-3}{2x-1}}$
Here, the quotient is 2x2 – 5x + 2, and remainder is -1
Thus, the quotient in fraction form is ${2x^{2}-5x+2+\left( \dfrac{-1}{2x-1}\right)}$ = ${2x^{2}-5x+2-\dfrac{1}{2x-1}}$
![]()
Find the quotient and remainder of the following polynomial division:
(6x3 – 4x2 + 3x – 5) ÷ (2x – 1)
Solution:
![]()
Given, ${\dfrac{6x^{3}-4x^{2}+3x-5}{2x-1}}$
Thus, the quotient is ${3x^{2}-\dfrac{x}{2}+\dfrac{5}{4}}$, and the remainder is ${-\dfrac{15}{4}}$
Problem: Dividing a QUARTIC POLYNOMIAL by a polynomial
![]()
Divide the following polynomial division:
(5x4 + 3x3 – 2x2 + x – 4) ÷ (x2 – x + 2)
Solution:
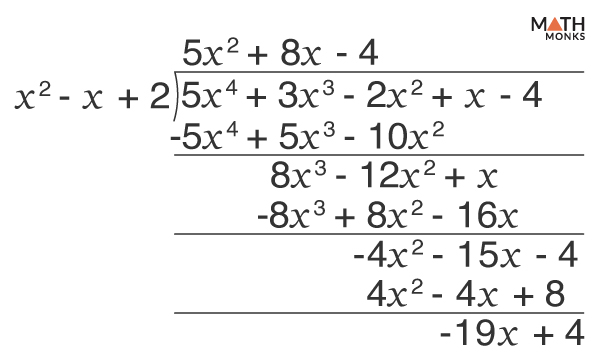
Given, ${\dfrac{5x^{4}+3x^{3}-2x^{2}+x-4}{x^{2}-x+2}}$
Thus, the quotient is 5x2 + 8x – 4, and the remainder is -19x + 4
Problem: Dividing polynomials of the SAME DEGREES
![]()
Solve: ${\dfrac{3x^{2}+5x-2}{x^{2}+2x+1}}$
Solution:
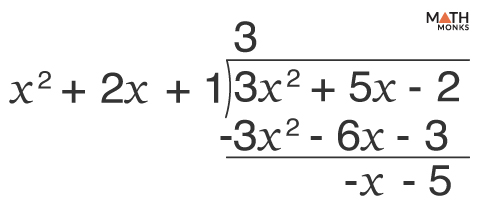
Given, ${\dfrac{3x^{2}+5x-2}{x^{2}+2x+1}}$
Thus, the quotient is 3, and the remainder is -x – 5
