- Shapes
- Rectangle
- Square
- Circle
- Triangle
- Rhombus
- Squircle
- Oval
- Hexagon
- Pentagon
- Trapezoid
- Kite
- Parallelogram
- Quadrilateral
- Polygon
- Nonagon
- Heptagon
- Decagon
- Octagon
- Ellipse
- Parallelepiped
- Tetrahedron
- Cylinder
- Prism
- Sphere
- Pyramid
- Frustum
- Polyhedron
- Dodecagon
- Dodecahedron
- Octahedron
- Torus
- Cube
- Cone
- Hyperbola
- Rectangular Prism
- Fibonacci Sequence
- Golden Ratio
- Parabola
- Worksheets
- Calculators
- Angle
- Arithmetic
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Decimal
- Order of Operations (PEMDAS)
- Scientific Notation
- Symmetry
- Fractions
- Triangular Number
- Complex Number
- Binary Number System
- Logarithm
- Binomial Theorem
- Quartic Function
- Mathematical Induction
- Group Theory
- Modular Arithmetic
- Euler’s Number
- Inequalities
- Sets
- De Morgan’s Laws
- Transcendental Numbers
- About Us
Search

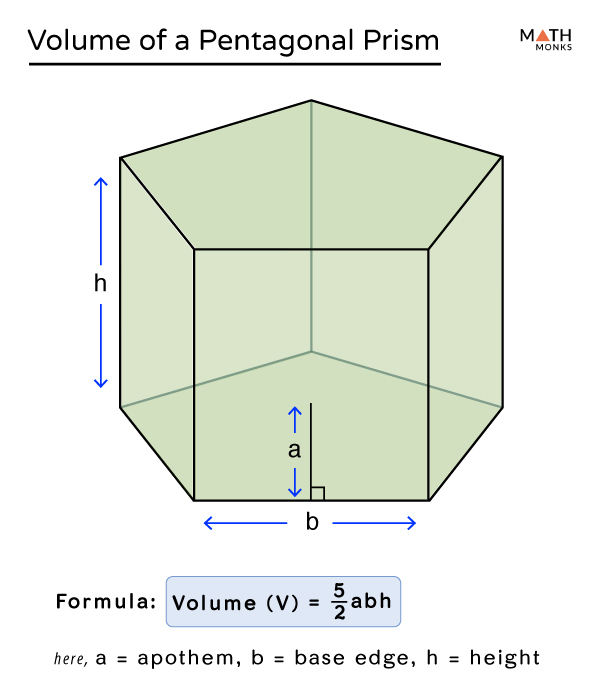
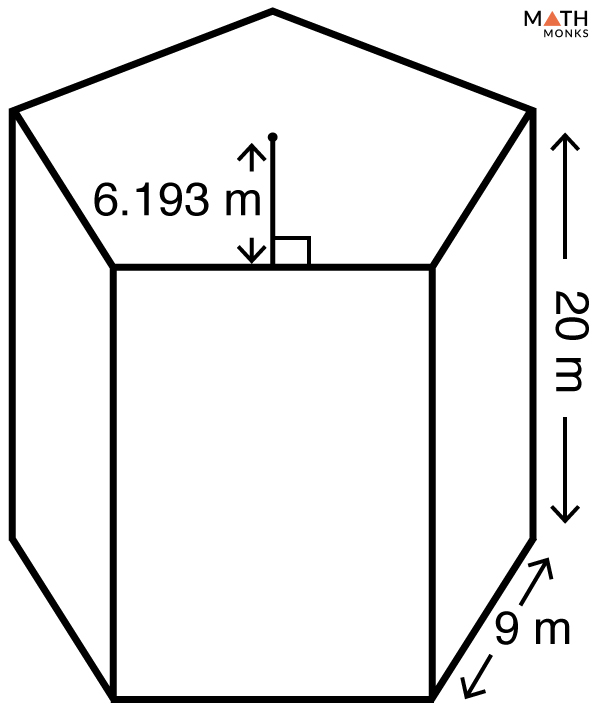 Find the volume of a regular pentagonal prism given in the figure.
Find the volume of a regular pentagonal prism given in the figure.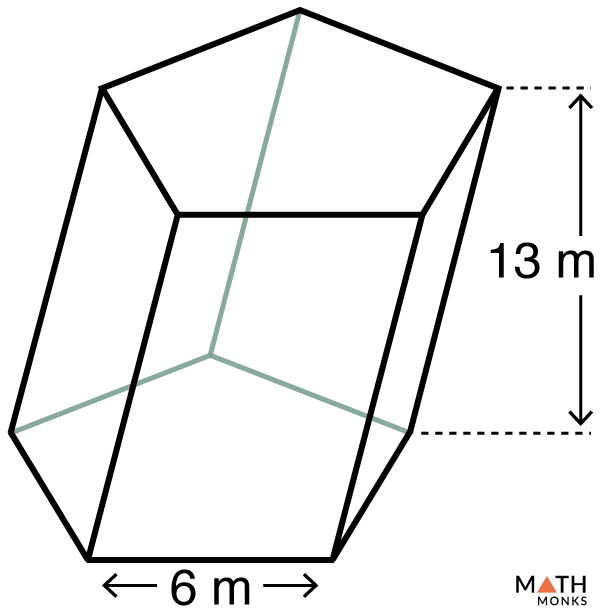 Find the volume of the oblique pentagonal prism given in the figure.
Find the volume of the oblique pentagonal prism given in the figure.