Table of Contents
Last modified on August 3rd, 2023
The volume of a trapezoidal prism is the space it occupies in the three-dimensional plane. It is measured in cubic units such as m3, cm3, mm3, ft3.
The formula is given below:
Let us solve some examples to understand the concept better.
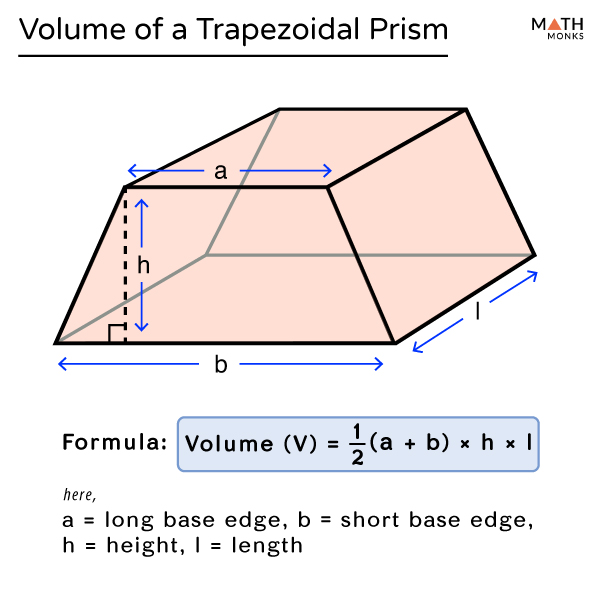
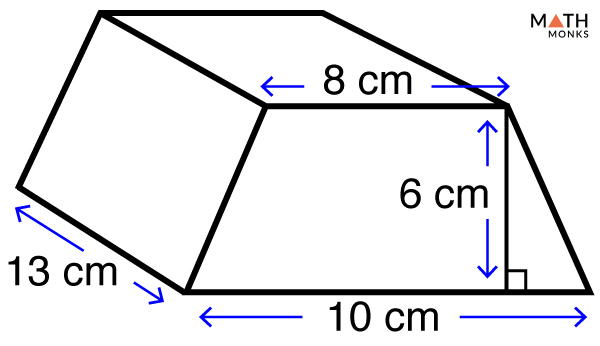Find the volume of a trapezoidal prism given in the figure.
As we know,
${Volume\left( V\right) =\dfrac{1}{2}\left( a+b\right) \times h\times l}$, here a = 10 cm, b = 8 cm, h = 6 cm, l = 13 cm
${\therefore V=\dfrac{1}{2}\times \left( 10+8\right) \times 6\times 13}$
= 702 cm3
Finding the volume of a trapezoidal prism when BASE AREA and LENGTH are known
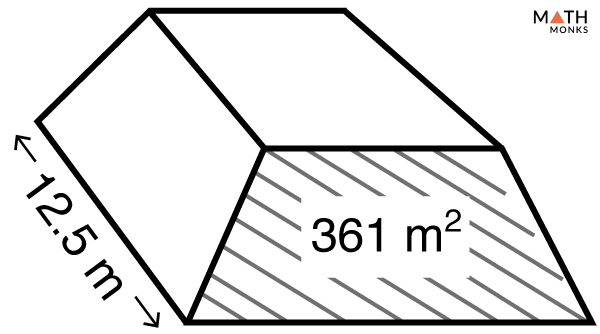Find the volume of a trapezoidal prism given in the figure, whose base area is 361 m2 and length is 12.5 m.
Here we will use an alternative formula.
Volume (V) = Base Area × l, here base area = 361 m2, l = 12.5 m
∴V = 361 × 12.5
= 4512.5 m3
Finding the volume of an oblique trapezoidal prism when BASE AREA and LENGTH are known
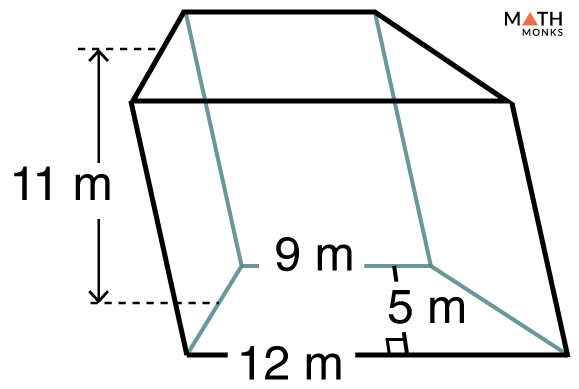Find the volume of an oblique trapezoidal prism given in the figure.
As we know,
Volume of a right trapezoidal prism with length ‘l’ = Volume of oblique trapezoidal prism length ‘l’
${Volume\left( V\right) =\dfrac{1}{2}\left( a+b\right) \times h\times l}$, here a = 12 m, b = 9 m, h = 5 m, l = 11 m
${\therefore V=\dfrac{1}{2}\times \left( 12+9\right) \times 5\times 11}$
= 577.5 m3
Last modified on August 3rd, 2023
This is an interesting and informative post on the volume of a trapezoidal prism. It provides a clear definition, formula, and examples to help readers understand this concept better. Thanks for sharing!